
Закон інерції квадратичних форм
|
|
Нехай  - квадратична функція на скінченновимірному векторному просторі
- квадратична функція на скінченновимірному векторному просторі 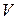 над полем
над полем 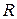 . Тоді в будь-якому базисі простору вона задається деякою квадратичною формою. Квадратичну функцію можна звести до канонічного вигляду. Це означає, що шукається базис, у якому функція
. Тоді в будь-якому базисі простору вона задається деякою квадратичною формою. Квадратичну функцію можна звести до канонічного вигляду. Це означає, що шукається базис, у якому функція  задається канонічною квадратичною формою. Але цей базис можна знайти різними способами. Тому для даної квадратичної функції існує багато таких базисів і багато канонічних квадратичних форм. Але для всіх цих форм виконується закон інерції квадратичних форм.
задається канонічною квадратичною формою. Але цей базис можна знайти різними способами. Тому для даної квадратичної функції існує багато таких базисів і багато канонічних квадратичних форм. Але для всіх цих форм виконується закон інерції квадратичних форм.
Теорема (закон інерції квадратичних форм). Незалежно від способу зведення квадратичної функції на скінченновимірному просторі до канонічного вигляду у відповідних канонічних квадратичних формах число додатних коефіцієнтів, число від’ємних коефіцієнтів, а тому і число ненульових є величинами сталими.
Доведення. Нехай  - квадратична функція на скінченновимірному просторі
- квадратична функція на скінченновимірному просторі 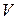 ,
,  - базиси простору, в яких функція
- базиси простору, в яких функція  задається канонічними квадратичними формами. Припустимо, що в базисі
задається канонічними квадратичними формами. Припустимо, що в базисі  функції
функції  відповідає квадратична форма:
відповідає квадратична форма:

 У базисі
У базисі  функції
функції  відповідає квадратична форма:
відповідає квадратична форма:

Доведемо, що 
Покажемо спочатку, що  Оскільки в базисі
Оскільки в базисі  квадратична функція
квадратична функція  задається канонічною квадратичною формою, то в цьому базисі матриця квадратичної функції діагональна. На діагоналі матриці стоять коефіцієнти при квадратах змінних у квадратичній формі. Тобто, ранг цієї матриці дорівнює
задається канонічною квадратичною формою, то в цьому базисі матриця квадратичної функції діагональна. На діагоналі матриці стоять коефіцієнти при квадратах змінних у квадратичній формі. Тобто, ранг цієї матриці дорівнює  . Аналогічно, в базисі
. Аналогічно, в базисі  квадратичній функції
квадратичній функції  відповідає діагональна матриця, ранг якої дорівнює
відповідає діагональна матриця, ранг якої дорівнює  . Вище було показано, що ранг матриці білінійної функції не залежить від вибору базису, тому
. Вище було показано, що ранг матриці білінійної функції не залежить від вибору базису, тому 
Покажемо тепер, що 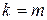 . Доведемо це від супротивного. Припустимо, що
. Доведемо це від супротивного. Припустимо, що  і, для визначеності, покладемо, що
і, для визначеності, покладемо, що  . Визначимо підпростори:
. Визначимо підпростори:

Тоді
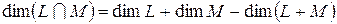 ,
,
але

а тому
 .
.
Тобто, існує ненульовий вектор 
Оскільки  , то вектор
, то вектор  лінійно виражається через вектори
лінійно виражається через вектори  :
:
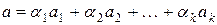 ,
,
тобто, в базисі простору  вектор
вектор  задається такими координатами:
задається такими координатами:

А тому
 .
.
Оскільки  , то серед координат
, то серед координат  існує принаймні одна ненульова і, враховуючи, що
існує принаймні одна ненульова і, враховуючи, що  одержуємо, що
одержуємо, що  . Оскільки
. Оскільки  , то вектор
, то вектор  лінійно виражається через вектори
лінійно виражається через вектори  :
:
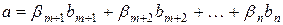 .
.
Тобто, в базисі  вектору
вектору  відповідають такі координати:
відповідають такі координати:
 .
.
Тоді


оскільки  . Приходимо до суперечності:
. Приходимо до суперечності:

Отже,  і, оскільки, за доведеним,
і, оскільки, за доведеним, 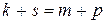 , то
, то  .
.
Зауваження. Під рангом квадратичної функції розуміється ранг її полярної білінійної функції. Ранг білінійної функції дорівнює рангу її матриці в будь-якому базисі. Якщо квадратична функція зводиться до канонічного вигляду, то знаходиться базис, у якому квадратичній функції відповідає діагональна матриця і канонічна квадратична форма. На діагоналі матриці стоять коефіцієнти при квадратах змінних у квадратичній формі. Звідси випливає, що ранг квадратичної функції співпадає з числом ненульових коефіцієнтів у канонічній квадратичній формі, яка відповідає цій квадратичній функції.
Додатні квадратичні функції
Означення. Квадратична функція  на векторному просторі
на векторному просторі 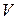 над полем
над полем 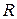 називається додатною, якщо для
називається додатною, якщо для 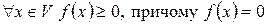 тоді і тільки тоді, коли
тоді і тільки тоді, коли 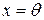 .
.
Нехай  - полярна симетрична білінійна функція, що породжує додатну квадратичну функцію
- полярна симетрична білінійна функція, що породжує додатну квадратичну функцію  , тоді
, тоді  задає на просторі
задає на просторі 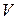 скалярний добуток.
скалярний добуток.
Дійсно, перевіримо виконання умов скалярного добутку:
1.  .
.
Це випливає з симетричності білінійної функції 
2. 
3. 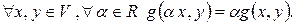
Виконання цих умов випливає з лінійності функції  за першим аргументом.
за першим аргументом.
4. 
 тоді і тільки тоді, коли
тоді і тільки тоді, коли 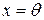 .
.
Умова виконується, оскільки 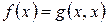 - додатна квадратична функція.
- додатна квадратична функція.
Критерій Сильвестера
Будемо казати, що матриця 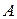 з дійсними елементами задовольняє умову Сильвестера, якщо всі її кутові мінори додатні.
з дійсними елементами задовольняє умову Сильвестера, якщо всі її кутові мінори додатні.
Тобто, якщо 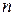 - порядок матриці, а
- порядок матриці, а  - всі кутові мінори матриці, то
- всі кутові мінори матриці, то 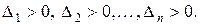
Теорема (критерій Сильвестера). Квадратична функція на скінченновимірному векторному просторі додатна тоді і тільки тоді, коли в деякому базисі простору її матриця задовольняє умову Сильвестера.
Доведення.Необхідність. Нехай  - додатна квадратична функція на скінченновимірному просторі
- додатна квадратична функція на скінченновимірному просторі 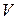 . Покажемо, що в будь-якому базисі
. Покажемо, що в будь-якому базисі 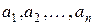 простору матриця квадратичної функції
простору матриця квадратичної функції
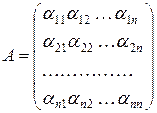
задовольняє умову Сильвестера.
Доведемо це індукцією за розмірністю 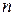 простору.
простору.
Нехай спочатку  , ненульовий вектор
, ненульовий вектор  утворює базис
утворює базис 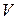 . Тоді в цьому базисі квадратична функція
. Тоді в цьому базисі квадратична функція  задається квадратичною формою:
задається квадратичною формою:
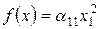 .
.
Припустимо, що  . Тоді
. Тоді 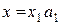 для деякого
для деякого 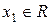 , причому
, причому  ;
; 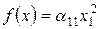 і, оскільки
і, оскільки  - додатна квадратична функція, то
- додатна квадратична функція, то 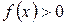 . Але
. Але 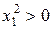 , тому
, тому
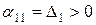 .
.
Припустимо тепер, що твердження виконується для всіх просторів розмірності менше 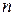
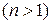 , тобто, будь-яка квадратична функція в будь-якому базисі такого простору задається матрицею, яка задовольняє умову Сильвестера. І нехай
, тобто, будь-яка квадратична функція в будь-якому базисі такого простору задається матрицею, яка задовольняє умову Сильвестера. І нехай  ,
,  - деяка квадратична функція на
- деяка квадратична функція на 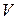 ,
, 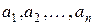 - фіксований базис простору, в якому функції
- фіксований базис простору, в якому функції  відповідає матриця
відповідає матриця
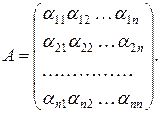
Покажемо, що 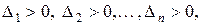 де
де  - всі кутові мінори матриці
- всі кутові мінори матриці 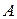 . У цьому базисі квадратична функція задається такою квадратичною формою:
. У цьому базисі квадратична функція задається такою квадратичною формою:
 .
.
Цю квадратичну форму можна переписати так:
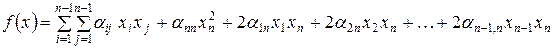 .
.
Визначимо підпростір 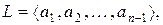 і нехай
і нехай 
 .
.
Тоді  - квадратична форма від змінних
- квадратична форма від змінних  , яка при фіксованому базисі
, яка при фіксованому базисі  підпростору
підпростору 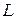 задає на цьому підпросторі деяку квадратичну функцію
задає на цьому підпросторі деяку квадратичну функцію  причому
причому 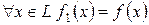 . Тому, оскільки функція
. Тому, оскільки функція  додатна, то і функція
додатна, то і функція 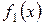 додатна. Але
додатна. Але
 ,
,
тому, за припущенням індукції, матриця квадратичної функції 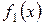 на підпросторі
на підпросторі 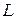 у базисі
у базисі  задовольняє умову Сильвестера. Ця матриця співпадає з матрицею кутового мінору
задовольняє умову Сильвестера. Ця матриця співпадає з матрицею кутового мінору  матриці
матриці 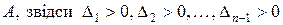 .
.
Залишається показати, що 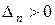 . Зводимо квадратичну функцію
. Зводимо квадратичну функцію  до канонічного вигляду. При цьому знаходимо базис простору
до канонічного вигляду. При цьому знаходимо базис простору 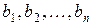 , у якому функції
, у якому функції  відповідає діагональна матриця:
відповідає діагональна матриця:
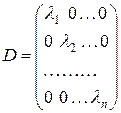 .
.
Зрозуміло, що
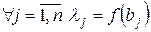 ,
,
і, оскільки
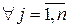
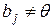 ,
,
то
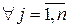
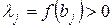 .
.
Якщо 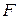 - матриця переходу від базису
- матриця переходу від базису 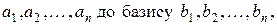 то
то
 ,
,
причому 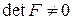 . Тоді
. Тоді
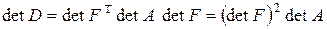 ,
,
і, оскільки
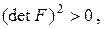
а
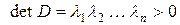 ,
,
то
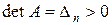 .
.
Достатність. Припустимо, що  - квадратична функція на скінченновимірному векторному просторі
- квадратична функція на скінченновимірному векторному просторі 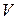 , і в базисі
, і в базисі 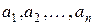 простору її матриця
простору її матриця 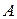 задовольняє умову Сильвестера. Тоді ця матриця задовольняє і умову Якобі, а тому існує базис
задовольняє умову Сильвестера. Тоді ця матриця задовольняє і умову Якобі, а тому існує базис 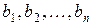 простору, в якому функція
простору, в якому функція  задається канонічною квадратичною формою:
задається канонічною квадратичною формою:
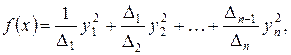
де  - всі кутові мінори матриці
- всі кутові мінори матриці 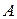 . За умовою теореми, всі коефіцієнти цієї квадратичної форми додатні. Припустимо, що
. За умовою теореми, всі коефіцієнти цієї квадратичної форми додатні. Припустимо, що 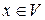 -довільний вектор, який у базисі
-довільний вектор, який у базисі 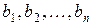 задається такими координатами:
задається такими координатами:  . Тоді
. Тоді
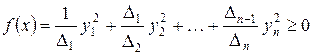 .
.
Якщо  , то серед координат
, то серед координат 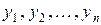 є ненульові, а тому
є ненульові, а тому 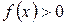 , тобто, функція
, тобто, функція  додатна.
додатна.
Зауваження. В процесі доведення останньої теореми фактично було показано, що матриця додатної квадратичної функції на скінченновимірному просторі в будь-якому базисі задовольняє умову Сильвестера.
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |