
Електричне поле у діелектриках
|
|
Основні формули
1. Диполь – це система двох однакових за модулем і протилежних за знаком зарядів, які розміщені на деякій відстані один від одного.
Електричний момент р диполя це вектор, який напрямлений від негативного заряду до позитивного і який дорівнює добутку заряду |q| на вектор 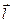 , що проведений від негативного заряду до позитивного та називається плечем диполя, тобто
, що проведений від негативного заряду до позитивного та називається плечем диполя, тобто
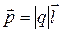 .
.
Диполь має назву точкового, якщо плече l диполя значно менше відстані r від центра диполя до точки, у якій визначається дія диполя (l<<r).
2. Напруженість поля точкового диполя визначається за формулою
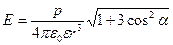 ,
,
де  – електричний момент диполя;
– електричний момент диполя;
r – абсолютне значення радіуса вектора, який проведений від центра диполя до точки, напруженість поля в якій визначається;
 – кут між радіусом-вектором r та плечем l диполя.
– кут між радіусом-вектором r та плечем l диполя.
Напруженість поля точкового диполя у точці, яка лежить на осі диполя (  = 0)
= 0)
 ,
,
і в точці, яка лежить на перпендикулярі до плеча диполя, що проведений із його середини (а = 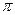 /2)
/2)
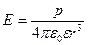 .
.
3. Потенціал поля точкового диполя на відстані r від диполя
 .
.
4. Потенціал поля точкового диполя у точці, яка лежить на осі диполя (  = 0)
= 0)
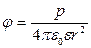 ,
,
і в точці, яка лежить на перпендикулярі до плеча диполя, який проведений із його середини (  =
= 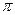 /2)
/2)
 .
.
Напруженість і потенціал неточкового диполя визначаються як для системи зарядів.
Механічний момент, який діє на диполь з електричним моментом  , розміщеним в однорідному електричному полі з напруженістю Е
, розміщеним в однорідному електричному полі з напруженістю Е
 або
або 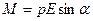 ,
,
де а – кут між напрямками векторів  та
та  .
.
У неоднорідному електричному полі, окрім механічного моменту (пари сил), на диполь діє ще деяка сила. У випадку поля, яке має симетрію відносно осі х, ця сила виражається співвідношенням
 ,
,
де 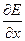 – частинна похідна напруженості поля, яка характеризує ступінь неоднорідності поля у напрямку осі х.
– частинна похідна напруженості поля, яка характеризує ступінь неоднорідності поля у напрямку осі х.
При а > 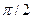 сила Fх позитивна. Це означає, що під її дією диполь втягується в область сильного поля.
сила Fх позитивна. Це означає, що під її дією диполь втягується в область сильного поля.
5. Електричне зміщення D пов'язане з напруженістю Е електричного поля таким співвідношенням
 .
.
Це співвідношення може бути застосованим лише для ізотропних діелектриків.
6. Потік вектора електричного зміщення визначається аналогічно потоку вектора напруженості електричного поля:
– у випадку однорідного поля
 ;
;
– у випадку неоднорідного поля
 ,
,
де Dn – проекція вектора  на напрямок нормалі до елемента поверхні, площа якої дорівнює dS.
на напрямок нормалі до елемента поверхні, площа якої дорівнює dS.
7. Теорема Гаусса для поля в діелектриках. Потік вектора електричного зміщення через будь-яку замкнену поверхню дорівнює алгебраїчній сумі сторонніх зарядів, які охоплені цією поверхнею:
 ,
,
де п – кількість сторонніх зарядів, які охоплені замкнутою поверхнею.
Провідники в електричному полі
Основні формули
1. Електроємність ізольованого провідника або конденсатора
 ,
,
де dq – заряд, переданий провіднику (конденсатору);
d  – зміна потенціалу, яка викликана цим зарядом.
– зміна потенціалу, яка викликана цим зарядом.
2. Електроємність ізольованої провідної сфери радіусом R, яка розміщена у нескінченному середовищі з діелектричною проникністю 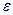
 .
.
Якщо сфера порожня і заповнена діелектриком, то електроємність її від цього не змінюється.
3. Електроємність плоского конденсатора
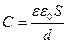 ,
,
де S – площа кожної з пластин;
d – відстань між ними;
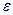 – діелектрична проникність діелектрика, який заповнює простір між пластинами.
– діелектрична проникність діелектрика, який заповнює простір між пластинами.
Електроємність плоского конденсатора, який заповнений n шарами діелектрика товщиною d кожний, діелектричні проникності яких 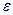 і (шаруватий конденсатор)
і (шаруватий конденсатор)
 .
.
4. Електроємність сферичного конденсатора (дві концентричні сфери радіусами R1 і R2, простір між якими заповнено діелектриком з діелектричною проникністю 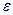 )
)
 .
.
5 Електроємність циліндричного конденсатора (два коаксіальних циліндри довжиною l i радіусами R1 і R2, простір між якими заповнено діелектриком з діелектричною проникністю 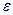 )
)
 .
.
6. Електроємність послідовно з'єднаних конденсаторів визначається формулою
 ,
,
де п – кількість конденсаторів;
У випадку двох конденсаторів
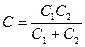 .
.
У випадку п однакових конденсаторів з електроємністю СІ кожний
 .
.
7. Електроємність паралельно з'єднаних конденсаторів:
 ,
,
де п – кількість конденсаторів.
У випадку двох конденсаторів:
 .
.
У випадку п однакових конденсаторів з електроємністю С2кожний
С = nC2.
Енергія електричного поля
Основні формули
1. Енергія зарядженого провідника виражається через заряд q, потенціал  та ємність C провідника такими співвідношеннями:
та ємність C провідника такими співвідношеннями:
 .
.
2. Енергія зарядженого конденсатора
 ,
,
де С – електроємність конденсатора;
U – різниця потенціалів на його пластинах.
3. Об'ємна густина енергії (енергія електричного поля, що припадає на одиницю об'єму)
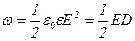 ,
,
де Е – напруженість електричного поля в середовищі з діелектричною проникністю  ;
;
 – вектор електричного зміщення.
– вектор електричного зміщення.
Приклади розв’язання задач
Приклад 1. У вершинах квадрата перебувають однакові точкові заряди 30 нКл. Який негативний заряд треба помістити в центрі квадрата, щоб зазначена система зарядів перебувала в рівновазі?
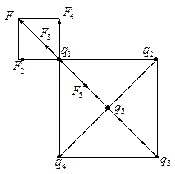 Дано:
Дано:
q1 = q2 = q3 = q4 = 30 нКл = 30.10-9 Кл.
_______________________________
q5 = ?
Розв’язання. Всі заряди, розташовані у вершинах квадрата, перебувають в однакових умовах. Тому досить з'ясувати, який заряд слід помістити в центр квадрата, щоб який-небудь із чотирьох зарядів, наприклад q1, перебував у рівновазі. Заряд q1 буде перебувати в рівновазі, якщо векторна сума діючих на нього сил дорівнює Рисунок 6
нулю (рис.6)
 0, ( 1)
0, ( 1)
де  ,
,  ,
,  ,
,  – сили, з якими відповідно діють на заряд q1 заряди q2 , q3 , q4, q5;
– сили, з якими відповідно діють на заряд q1 заряди q2 , q3 , q4, q5;
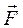 =
=  +
+  – рівнодійна сил
– рівнодійна сил  та
та 
 .
.
За законом Кулона, маючи на увазі, що q1 = q2 = q3 = q4 = q, одержимо
F2 = F4 =  , ( 2)
, ( 2)
F3 = 
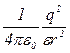 , ( 3)
, ( 3)
F5 =  , ( 4)
, ( 4)
де a – сторона квадрата;
r = a  – діагональ квадрата.
– діагональ квадрата.
Як видно з рис. 6, рівнодійна сил  й
й  за напрямком збігається із силою F3 і за модулем дорівнює F =
за напрямком збігається із силою F3 і за модулем дорівнює F =  . З урахуванням цього твердження векторну рівність (1) можна замінити скалярною
. З урахуванням цього твердження векторну рівність (1) можна замінити скалярною
F + F3 - F5 = F2 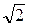 +F3 -F5 . ( 5)
+F3 -F5 . ( 5)
Рівність (5) з урахуванням (2) – (4) матиме вигляд
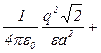

 = 0 .
= 0 .
Звідки
 q .
q .
Здійснивши обчислення, одержимо
 3.10-8 Кл = 2,87 . 10-8 Кл.
3.10-8 Кл = 2,87 . 10-8 Кл.
Слід зазначити, що рівновага системи зарядів буде нестійкою.
 Приклад 2. Два точкових заряди 2 нКл і -1 нКл перебувають у повітрі на відстані 5 см один від одного. Визначити напруженість і потенціал електричного поля в точці, віддаленої від першого заряду на відстань 6 см і від другого заряду на відстань 4 см.
Приклад 2. Два точкових заряди 2 нКл і -1 нКл перебувають у повітрі на відстані 5 см один від одного. Визначити напруженість і потенціал електричного поля в точці, віддаленої від першого заряду на відстань 6 см і від другого заряду на відстань 4 см.
Дано:
q1 = 2 нКл
q2 = - 1 нКл
d = 5 см
r1 = 6 см
r2 = 4 см
____________
Е – ?
j – ?
Рисунок 7
Розв’язання. Відповідно до принципу суперпозиції електричних полів кожен заряд створює поле незалежно від наявності в просторі інших зарядів. Напруженість результуючого поля  . Напруженості полів, створюваних у повітрі (e = 1) зарядами q1 й q2 визначають за формулами:
. Напруженості полів, створюваних у повітрі (e = 1) зарядами q1 й q2 визначають за формулами:
E1 = 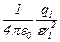 , ( 1)
, ( 1)
E2 = 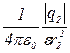 . (2)
. (2)
Напрямки векторів  і
і 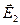 зазначені на рис.7. Модуль вектора E знайдемо за теоремою косинусів
зазначені на рис.7. Модуль вектора E знайдемо за теоремою косинусів
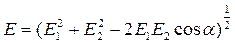 , (3)
, (3)
де a – кут між векторами  і
і 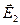 .
.
З рис.7 видно, що 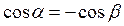 .
.
Отже,
 . (4)
. (4)
Із трикутника зі сторонами r1, r2, d за теоремою косинусів знаходимо
cos b = ( r12 + r22 - d2) / (2r1r2).
Обчислимо cos  окремо
окремо
cosb =  .
.
Виразимо всі величини в одиницях СІ: q1 = 2.10-9 Кл, q2 = -10-9 Кл, r1 = 6.10-2 м, r2 = 4.10-2 м, 1/4pe0 = 9.109 м/Ф, e = 1.
Зробивши обчислення за формулами (1), (2), (4), (5), одержимо:
E1 =  B/м,
B/м,
E2 = 
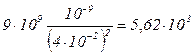 B/м.
B/м.
При обчисленні Е2 знак заряду q2 опущений, тому що знак мінус визначає напрямок вектора 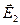 , а напрямок
, а напрямок 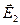 був врахований при його графічному зображенні (рис.7).
був врахований при його графічному зображенні (рис.7).
 .
.
За принципом суперпозиції потенціал результуючого поля, створюваного зарядами q1 й q2, дорівнює алгебраїчній сумі потенціалів j1 та j2, тобто j = j1 + j2 або
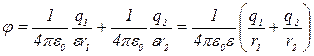 . (5)
. (5)
Зробивши обчислення, одержимо
 .
.
Приклад 3. На тонкій нитці, вигнутій по дузі кола радіусом 6 см, рівномірно розподілений заряд з лінійною густиною 20нКл/м. Визначити напруженість і потенціал електричного поля, створюваного розподіленим зарядом у точці, яка збігається із центром кривизни дуги, якщо довжина нитки становить 1/3 довжини кола.
 Дано:
Дано:
R = 6 см
 = 20 нКл/м
= 20 нКл/м
l = 2/3 R
___________
Е - ?  - ?
- ?
Розв’язання. Виберемо осі координат так, щоб початок координат збігався із центром кривизни дуги, а вісь ОY була б розташована симетрично до кінців дуги (рис.8). Рисунок 8
Розіб'ємо нитку на елементарні ділянки й виділимо елемент довжиною dl із зарядом dq =  dl. Цей заряд можна розглядати як точковий.
dl. Цей заряд можна розглядати як точковий.
Визначимо напруженість електричного поля в точці О. Для цієї точки напруженість поля, створюваного зарядом dq, дорівнює
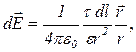
де  – радіус-вектор, спрямований від елемента dl у точку О.
– радіус-вектор, спрямований від елемента dl у точку О.
Розіб'ємо вектор d  на складові
на складові 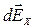 й
й  . Із умови симетрії випливає, що сума складових
. Із умови симетрії випливає, що сума складових  від всіх елементарних ділянок нитки дорівнює нулю й результуючий вектор
від всіх елементарних ділянок нитки дорівнює нулю й результуючий вектор  буде спрямований уздовж осі OY. В цьому випадку напруженість поля визначиться так
буде спрямований уздовж осі OY. В цьому випадку напруженість поля визначиться так
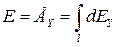 , (1)
, (1)
де dEY = dЕ sin a.
Оскільки r = R й dl = Rd  , то
, то
dEy=  sin
sin  =
=  sin
sin  d
d  . (2)
. (2)
Після підстановки (2) в (1), проведемо інтегрування в межах зміни кута від 0 до 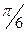 , попередньо помноживши цей інтеграл на 2
, попередньо помноживши цей інтеграл на 2
E=  =
=  . (3)
. (3)
Знайдемо потенціал електричного поля у точці О. У цій точці потенціал поля, створеного точковим зарядом dq, дорівнює
 . (4)
. (4)
Потенціал результуючого поля одержимо шляхом інтегрування виразу (4) по довжині нитки
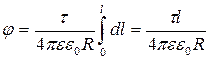 .
.
Оскільки l = 2 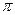 R / 3, то
R / 3, то
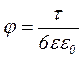 . (5)
. (5)
Виразимо всі величини в одиницях СІ: t = 2.10-8 Кл/м, R = 6.10-2 м, 1/4pe0 = 9.109 м/Ф, e = 1, e0 = 8,85.10-12 Ф/м.
Здійснивши обчислення за формулами (3) і (5), одержимо:
E =  В/м,
В/м,
 В.
В.
Приклад 4. Електричне поле створене довгим циліндром радіусом 1 см, рівномірно зарядженим з лінійною густиною заряду 20 нКл/м. Визначити роботу сил поля з переміщення точкового заряду 25 нКл із точки, що перебуває на відстані 1 см, у точку, що перебуває на відстані 3 см від поверхні циліндра в середній його частині.
Дано:
R = 1 см = 1.10-2 м
t = 20 нКл/м = 2.10-8 Кл/м
q = 25 нКл = 2,5. 10-8 Кл
a1 = 1 см = 1.10-2 м
a2 = 3 см = 3.10-2 м
_____________________
А - ?
Розв’язування. Робота сил поля з переміщення заряду дорівнює
А = q(j1 - j2).
Для знаходження різниці потенціалів скористаємося співвідношенням  j. Для поля з осьовою симетрією, яким є поле циліндра, можна записати
j. Для поля з осьовою симетрією, яким є поле циліндра, можна записати
Е = 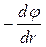 або
або 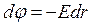 .
.
Інтегруючи цей вираз, знайдемо різницю потенціалів між двома точками, які відстоять від осі циліндра на відстанях r1 й r2
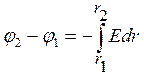 , (1)
, (1)
де r1 = a1 + R, r2 = a2 + R.
Оскільки циліндр довгий і точки взяті поблизу його середньої частини, то можна скористатися формулою напруженості поля, створюваного нескінченно довгим циліндром
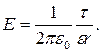 (2)
(2)
Підставивши (2) в (1), одержимо
 ln
ln 
або
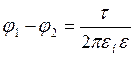 ln
ln  (3)
(3)
Таким чином,
 ln
ln 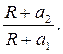
Перевіримо чи дає розрахункова формула одиницю роботи. Для цього в праву частину замість символів величин підставимо їх одиниці
 .
.
Виразимо всі величини в одиницях СІ: e = 1; t = 2.10-8 Кл/м; q = 2,5.10-8 Кл; 1/2peо = 2,9 109 м/Ф. Оскільки величини r2 й r1 входять у формулу (3) у вигляді відношення, то їх можна виразити в сантиметрах.
Виконавши необхідні розрахунки, одержимо
А = 2,5.10-8.2,9.109 .2. 10-8  = 6,2.10-6 Дж.
= 6,2.10-6 Дж. 
Приклад 5. Електричне поле створене тонкою нескінченно довгою ниткою, рівномірно зарядженою з лінійною густиною заряду  30 нКл/м. На відстані 20 см від нитки перебуває плоска кругла площадка радіусом 1 см. Визначити потік вектора напруженості електричного поля через площадку, якщо її площина складає кут 30о з лінією напруженості, яка проходить через середину площадки.
30 нКл/м. На відстані 20 см від нитки перебуває плоска кругла площадка радіусом 1 см. Визначити потік вектора напруженості електричного поля через площадку, якщо її площина складає кут 30о з лінією напруженості, яка проходить через середину площадки.
Дано:
 = 30 нКл/м
= 30 нКл/м
a = 20 см
R = 1 см
b = 30о
_____________
DNЕ - ?
Розв’язання. Поле, створюване ниткою (дуже тонким циліндром), є неоднорідним, тому воно змінюється в просторі
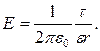 (1)
(1)
Потік вектора  дорівнює
дорівнює
 cos
cos 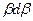 ,
,
де  – кут між векторами
– кут між векторами  й
й 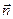 (рис.9). Оскільки лінійні розміри площадки малі в порівнянні з відстанню до нитки
(рис.9). Оскільки лінійні розміри площадки малі в порівнянні з відстанню до нитки  (а>>R), то Е в межах площадки змінюється незначно. Тому значення Е и cos
(а>>R), то Е в межах площадки змінюється незначно. Тому значення Е и cos  під знаком інтеграла можна замінити їх середніми значеннями <E> й <cos
під знаком інтеграла можна замінити їх середніми значеннями <E> й <cos  > і винести за знак інтеграла
> і винести за знак інтеграла
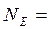 <E> <cos
<E> <cos  >
> 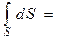 <E> <cos
<E> <cos  > S,
> S,
 де S =
де S = 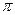 R2 .
R2 .
Замінюючи <E>й <cos  > їх наближеними значеннями ЕА й cos
> їх наближеними значеннями ЕА й cos  A, розрахованими для середньої точки А площадки, одержимо
A, розрахованими для середньої точки А площадки, одержимо
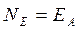 S cos
S cos  A =EA
A =EA 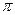 R2 cos
R2 cos  A . (2)
A . (2)
З рис.10 видно, що
cos  A = cos(90о -
A = cos(90о -  ) =sin
) =sin  .
.
З урахуванням цього формула (2) матиме
вигляд
 sin
sin 
 sin
sin  .
.
Рисунок 9
Виразимо всі величини в одиницях СІ: t = 3.10-8 Кл/м; e = 1; a = 0,2 м; R = 10-2 м; 1/2peо = 2,9.109 м/Ф.
Зробивши обчислення, одержимо
 B.м.
B.м.
Приклад 6. Електрон рухається в однорідному електричному полі вздовж силової лінії. У деякій точці поля з потенціалом 100 В електрон мав швидкість 4 Мм/с. Визначити потенціал точки поля, дійшовши до якої, електрон втратить половину своєї швидкості.
Дано:
j1 = 100 В
 1 = 4 Мм/с = 4.106 м/c
1 = 4 Мм/с = 4.106 м/c
 2 = 2 Мм/с = 2.106 м/c
2 = 2 Мм/с = 2.106 м/c
___________________
j2 – ?
Розв’язання. Через відсутність сил тертя повна механічна енергія електрона не змінюється, тобто W =  = const,
= const,
де 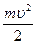 – кінетична й (- еj) – потенціальна енергія електрона.
– кінетична й (- еj) – потенціальна енергія електрона.
Повна енергія на початку руху
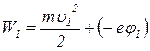 , (1)
, (1)
наприкінці руху з урахуванням того, що  2 =
2 =  1/2,
1/2,
 . (2)
. (2)
Прирівнявши вирази (1) і (2), одержимо для потенціалу
 .
.
Виразимо всі величини в одиницях СІ:  1 = 4.106 м/с; m = 9,1.10-31 кг; е = 1,6.10-19 Кл.
1 = 4.106 м/с; m = 9,1.10-31 кг; е = 1,6.10-19 Кл.
Виконавши обчислення, одержимо
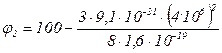 = 66 В .
= 66 В .
Можливий й інший підхід до розв’язання. Зміна кінетичної енергії частинки дорівнює роботі результуючої сили, тобто
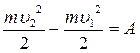 .
.
Оскільки електрон гальмується силами поля, то А = - е(j1 - j2).
Приклад 7. Сила взаємного притягання пластин плоского повітряного конденсатора 50 мН. Площа кожної пластини 200 см2. Визначити об'ємну густину енергії поля конденсатора.
Дано:
F = 50 мН = 5.10-2 Н
S = 200 см2 = 2.10-2 м2
__________________
w - ?
Розв’язання. Об'ємна густина енергії поля конденсатора
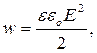 (1)
(1)
де Е =s/ee0 – напруженість електричного поля між пластинами конденсатора;
s – поверхнева густина заряду на пластинах.
Підставивши вираз для Е в (1), одержимо
 (2)
(2)
Знайдемо силу взаємного притягання пластин. Заряд q = sS однієї пластини перебуває в полі напруженістю Е1 = s / 2ee0, створеному зарядом іншої пластини конденсатора. Отже, на заряд першої пластини діє сила
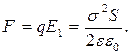 (3)
(3)
Виразивши s2 з формули (3) і підставивши її в (2), одержимо
w = F / S
Виразимо всі величини в одиницях СІ: F = 5.102 Н, S = 2.10-2 м2.
Виконавши необхідні обчислення, одержимо
 Дж/м3.
Дж/м3.
Приклад 8. Між пластинами плоского конденсатора, зарядженого до різниці потенціалів 600 В, перебувають два шари діелектриків – скло товщиною 5 мм та ебоніт товщиною 3 мм. Площа кожної пластини 200 см2. Визначити: а) напруженість електричного поля, індукцію й спад напруги в кожному шарі; б) електричну ємність конденсатора.
Дано:
U = 600 В
скло,
d1 = 5 мм = 5.10-3 м
ебоніт
d2 = 3 мм = 3.10‑ 3 м
S = 200 см2 = 2.10-2 м2
________________
Е – ? D – ?
U 1– ? U2 – ?
С – ?
Розв’язання. При переході через межу поділу діелектриків нормальна складова вектора  в обох шарах діелектриків має однакові значення D1n = D2n.
в обох шарах діелектриків має однакові значення D1n = D2n.
У конденсаторі силові лінії вектора  перпендикулярні до межі поділу діелектриків, отже, D1n = D1 й D2n = D2. Тому
перпендикулярні до межі поділу діелектриків, отже, D1n = D1 й D2n = D2. Тому
D1 = D2 = D. (1)
Врахувавши, що D = ee0Е, і скорочуючи на e0, з рівності (1) одержимо
e1E1 = e2Е2 , (2)
де Е1 й E2 – напруженості електричного поля в першому й у другому шарах діелектриків;
e1 й e2 – діелектричні проникності діелектриків.
Різниця потенціалів між пластинами конденсатора очевидно дорівнює сумі напруг на шарах діелектриків
U = U1 + U2 . (3)
У межах кожного шару поле однорідне, тому U1 = E1d1 й U2 = Е2d2. З урахуванням цього рівність (3) набуде вигляду
U = Е1d1 + E2d2. (4)
Розв’язавши спільно рівняння (2) і (4), одержимо
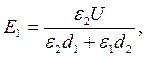
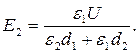
Виразимо всі величини в одиницях СІ: d1 = 5.10-3 м; d2 = 3.10-3 м; e1= 7; e2 = 3; e 0 = 8,85.10-12 Ф/м.
Виконавши необхідні обчислення, одержимо
 B/м;
B/м;
 B/м;
B/м;
 B;
B;
 B;
B;
 Кл/м2.
Кл/м2.
Визначимо ємність конденсатора
С =  , (5)
, (5)
де q =  S – заряд кожної пластини конденсатора. Враховуючи ту обставину, що поверхнева густина зарядів (на пластинах конденсатора чисельно дорівнює модулю електричного зміщення, тобто (
S – заряд кожної пластини конденсатора. Враховуючи ту обставину, що поверхнева густина зарядів (на пластинах конденсатора чисельно дорівнює модулю електричного зміщення, тобто (  = D), одержимо
= D), одержимо

Виконавши необхідні обчислення, одержимо
 пФ.
пФ.
Електричний струм
Основні формули
1. Сила постійного струму
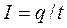 ,
,
де q – заряд, що пройшов через поперечний переріз провідника за час t.
2.Густина електричного струму є векторна величина, яка дорівнює відношенню сили струму до площі S поперечного перерізу провідника:
 ,
,
де k – одиничний вектор, який за напрямком збігається з напрямком руху позитивних носіїв заряду.
3. Опір однорідного провідника
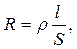
де 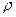 – питомий опір речовини провідника;
– питомий опір речовини провідника;
l – його довжина.
4. Провідність G провідника і питома провідність  речовини:
речовини:
 ,
,  .
.
5. Залежність питомого опору від температури
 ,
,
де 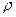 і
і 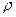 0 – питомі опори відповідно при t і 0°С;
0 – питомі опори відповідно при t і 0°С;
t – температура (за шкалою Цельсія);
 – температурний коефіцієнт опору.
– температурний коефіцієнт опору.
4. Опір послідовно з'єднаних провідників:
 .
.
Опір паралельно з'єднаних провідників
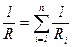 ,
,
де Rі – опір і-го провідника;
п – кількість провідників.
7. Закон Ома в інтегральній формі:
- для неоднорідної ділянки кола
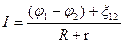 ;
;
- для однорідної ділянки кола ( 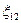 = 0)
= 0)
 ;
;
- для замкнутого кола (  =
= 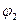 )
)
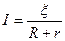 ,
,
де (  -
- 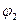 ) – різниця потенціалів на кінцях ділянки кола;
) – різниця потенціалів на кінцях ділянки кола;
 – е.р.с. джерел струму, що входять у цю ділянку;
– е.р.с. джерел струму, що входять у цю ділянку;
U – напруга на ділянці кола;
R – опір кола (ділянки кола);
 – е.р.с.усіх джерел струму замкнутого кола.
– е.р.с.усіх джерел струму замкнутого кола.
8. Правила Кірхгофа.
Перше правило: алгебраїчна сума сил струмів, що сходяться у вузлі, дорівнює нулю, тобто
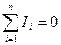 ,
,
де п – кількість струмів, що сходяться у вузлі.
Друге правило: у замкненому контурі алгебраїчна сума спадів напруги на всіх ділянках контуру дорівнює алгебраїчній сумі електрорушійних сил, тобто
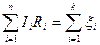 ,
,
де І – сила струму на і-й ділянці;
Rі – активний опір на і-й ділянці;
 – е.р.с. джерел струму на і-й ділянці;
– е.р.с. джерел струму на і-й ділянці;
п – кількість ділянок, що містять активний опір;
k – кількість джерел струму на всіх ділянках замкнутого контуру.
9. Робота, яка виконується електростатичним полем і сторонніми силами на ділянці кола постійного струму за час t
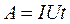 .
.
10. Потужність струму
 .
.
11. Закон Джоуля-Ленца
 ,
,
де Q – кількість теплоти, що виділяється на ділянках кола за час t.
Закон Джоуля - Ленца має місце за умови, що ділянка кола нерухома і в ній не здійснюються хімічні перетворення.
12. Густина струму j, середня швидкість  впорядкованого руху носіїв заряду та їх концентрація п пов'язані співвідношенням
впорядкованого руху носіїв заряду та їх концентрація п пов'язані співвідношенням
 ,
,
де q – елементарний заряд.
13. Закон Ома у диференціальній формі

де  – питома провідність провідника (
– питома провідність провідника (  ;
;
Е – напруженість електричного поля;
τ – середній час вільного руху носіїв струму;
m – масса електрона.
14. Закон Джоуля - Ленца у диференціальній формі
 ,
,
де  – об'ємна густина теплової потужності.
– об'ємна густина теплової потужності.
15. Закони електролізу Фарадея. Перший закон
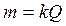 ,
,
де т – маса речовини, що виділилась на електроді під час проходження через електроліт електричного заряду Q;
k – електрохімічний еквівалент речовини.
Другий закон
 ,
,
де F – стала Фарадея (F = 96,5 кКл/моль);
 – молярна маса іонів даної речовини;
– молярна маса іонів даної речовини;
n – валентність іонів.
Об'єднаний закон
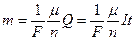
де І – сила струму, що проходить через електроліт;
t – час, протягом якого протікав струм.
16. Рухливість іонів
 ,
,
де <υ> – середня швидкість впорядкованого руху іонів;
Е – напруженість електричного поля.
17. Закон Ома у диференціальній формі для електролітів і газів при самостійному розряді в області, яка далека від насичення,
 ,
,
де Q – заряд іона;
п – концентрація іонів;
b+ і b- – рухливість відповідних іонів;
18. Густина струму насичення
 ,
,
де по – кількістьпар іонів, які створює іонізатор в одиниці об'єму за одиницю часу;
d – відстань між електродами (п0 =N/(Vt), де N – кількість пар іонів, що створює іонізатор за час t у просторі між електродами;
V – об'єм цього простору.
Приклади розв’язання задач
Приклад 1. Резистор опором 5 Ом, вольтметр і джерело струму з'єднані паралельно. Вольтметр по
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |