
Обробка результатів непрямих вимірювань
|
|
При непрямих вимірюваннях фізичної величини а її значення визначається за функціональною залежністю між нею та величинами аргументів, значення яких знайдене в результаті прямих вимірювань, тобто  . Метод оцінки величини a та похибки її вимірювання наступні. Для простоти розглянемо простий випадок, коли величини a є функцією одного аргументу:
. Метод оцінки величини a та похибки її вимірювання наступні. Для простоти розглянемо простий випадок, коли величини a є функцією одного аргументу:
 (13)
(13)
Розглянемо цю функцію поблизу  в межах інтервалу
в межах інтервалу  , де
, де  - оцінка величини х, а
- оцінка величини х, а  - похибка її вимірювання. Розкладемо функцію в ряд Тейлора, тобто представимо її у вигляді багаточлена:
- похибка її вимірювання. Розкладемо функцію в ряд Тейлора, тобто представимо її у вигляді багаточлена:
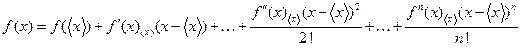 , (14)
, (14)
де  - похідна n – го порядку в точці
- похідна n – го порядку в точці  . Враховуючи, що похибка вимірювання величини х є малою величиною, зберігають лише члени першого порядку. Тоді:
. Враховуючи, що похибка вимірювання величини х є малою величиною, зберігають лише члени першого порядку. Тоді:
 (15)
(15)
Доданок із (15) є оцінкою значення величини а, тобто
 ,
,
де  - визначається з формулою
- визначається з формулою
 (16)
(16)
Другий доданок в (15) визначає похибку вимірювання величини а
 , (17)
, (17)
де 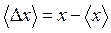 . Враховуючи, що похибка величини х може бути як із знаком “+”, так і з “-“, рівняння (17) записують у вигляді
. Враховуючи, що похибка величини х може бути як із знаком “+”, так і з “-“, рівняння (17) записують у вигляді
 (18)
(18)
У загальному випадку  , де
, де  , де і=1, 2,…, к
, де і=1, 2,…, к
Якщо похибки вимірювання величини  мають лише випадковий характер, то абсолютна похибка вимірювання величини а визначається за формулою
мають лише випадковий характер, то абсолютна похибка вимірювання величини а визначається за формулою
 ,
,
де  - частинні похідні при
- частинні похідні при  , а
, а  - похибки вимірювання величини
- похибки вимірювання величини  .
.
Результат непрямого вимірювання представляється у вигляді

Якщо вимірювана величина є функцією кількох змінних, похибки яких порівняно невеликі, то похибка непрямого вимірювання може бути визначена на основі формул таблиці. При цьому розраховують стандартну похибку  з довірчим інтервалом
з довірчим інтервалом  та довірчою імовірністю 68%.
та довірчою імовірністю 68%.
Лабораторне заняття №8
Вивчення температурної залежності електричного опору металів
1. Мета роботи.
Знайти залежність електричного опору металу від температури, визначити величину опору металевого провідника при температурі 0°С і величину температурного коефіцієнта опору.
Теоретичні відомості.
Електричні властивості кристалічних твердих тіл визначаються будовою їх кристалічної ґратки і характером сил, які діють між частинками твердого тіла, тобто типом хімічного зв'язку.
В залежності від того, які частинки перебувають у вузлах кристалічної ґратки та яка природа сил взаємодії між ними, розрізняють такі основні типи кристалів: іонні, атомні, металічні та молекулярні.
У вузлах ґратки іонних кристалів розміщуються іони різних знаків, сили взаємодії між якими переважно є електростатичними. Прикладом є гратка кам'яної солі NaCl, при створенні якої натрій віддає свій єдиний валентний електрон хлорові, якому не вистачає одного електрона для заповнення валентної оболонки (рис. 1).
 | |||
 | |||
Рис 1. Рис. 2.
Внаслідок цього обидва атоми стають іонами протилежних знаків та набувають стійких зовнішніх оболонок. Відсутність вільних носіїв заряду пояснює низьку електропровідність іонних кристалів.
У більшості випадків такі кристали є ізоляторами.
У вузлах ґратки атомних кристалів розташовані нейтральні атоми, зв'язок між якими здійснюється шляхом створення спільної пари валентних електронів (по одному електрону від кожного атома) і називається ковалентним. Такий зв'язок має місце, наприклад, між атомами в молекулі водню. При зближенні двох атомів водню траєкторії їхніх електронів перекриваються (рис. 2).
В області перекриття електрони перебувають під дією сильного притягання з боку обох ядер і починають рухатись по складним орбітам навколо обох ядер, тобто атоми виявляються зв'язаними спільною парою електронів.
При цьому виникає так звана обмінна взаємодія, вона лежить в основі ковалентного зв'язку і має квантову природу. Не зважаючи на те, що енергія зв'язку в атомних кристалах є значною, в багатьох з них можливе вивільнення електронів з ковалентних зв'язків. Під дією електричного поля вивільнені електрони стають носіями струму. Чим вища температура кристалу, тим більше виникає електронів провідності. Багато з таких кристалів (елементи з середньої групи таблиці Менделєєва, наприклад, германій та кремній і різні сполуки) є напівпровідниками.
У вузлах гратки металічних кристалів розташовані позитивні іони, між якими рухаються електрони. Вони створюють так званий електронний газ, який рівномірно заповнює простір між іонами. Цей тип гратки характерний для елементів (металів), у яких валентні електрони слабко зв'язані з ядром. При виникненні кристалічної гратки ці електрони легко відокремлюються від атомів і стають спільними для всього кристала.
Електронний газ зв'язує в міцну систему позитивно заряджені іони кристалу. Під впливом сил притягання з боку електронного газу і сил відштовхування між іонами останні розташовуються на деякій рівноважній відстані один від одного. Ця відстань відповідає мінімуму енергії в кристалі. Тіла з такою кристалічною граткою відзначаються високою електропровідністю, оскільки навіть слабке електричне поле викликає переміщення вільних електронів. При підвищені температури кристалу збільшується інтенсивність теплового коливального руху іонів, що затруднює напрямлений рух електронів в електричному полі.
У вузлах ґратки молекулярних кристалів знаходяться нейтральні молекули. Вони утримуються вандерваальсівськими силами, природа яких визначається взаємодією молекулярних диполів. За звичайних умов такі кристали електропровідністю не володіють і при підвищенні температури легко руйнуються. Молекулярну кристалічну гратку мають більшість органічних сполук.
Згідно з квантовою теорією енергія електронів в атомах квантується, тобто може приймати лише дискретні значення. Ці значення енергії відповідають енергетичним рівням. Якщо однакові атоми ізольовані один від одного, то вони мають однакові енергетичні рівні. При виникненні кристала відбувається зміна енергетичних рівнів у зв'язку із взаємодією атомів між собою. Якщо кристал складається з N атомів, то замість одного однакового для всіх атомів рівня виникає N дуже близьких за значеннями енергії рівнів, які не співпадають між собою. Так відбувається розщеплення енергетичного рівня на низку енергетичних рівнів.
Сукупність цих рівнів називається зоною енергетичних рівнів. Розщеплення енергетичних рівнів і виникнення зони енергетичних рівнів, яке має місце при зближенні атомів і виникненні кристала, здійснюється згідно з принципом Паулі, за яким на одному енергетичному рівні може перебувати не більше двох електронів з різною орієнтацією спінів.
Сукупність значень енергій, які можуть мати електрони в даному атомі (зони дозволених енергій) чергуються зі значеннями енергій, які електрони в даному атомі мати не можуть (зони заборонених енергій).
Ступінь розщеплення для різних рівнів неоднаковий. Рівні, заповнені близькими до ядра внутрішніми електронами, розщеплюються незначно, оскільки ці електрони слабко взаємодіють з електронами і ядрами інших атомів кристала. Така взаємодія є значною для валентних електронів, внаслідок чого їхні рівні розщеплюються сильніше, утворюючи так звану валентну зону. Ще помітнішим є розщеплення більш високих, ніж валентні, енергетичних рівнів, не зайнятих електронами в основному стані атома.
У кристалів різних типів ступінь заповнення валентної зони електронами різний, тому енергетичні зони розташовані по-різному, чим пояснюється різна за величиною їхня електропровідність.
При абсолютному нулі температури енергія кристала мінімальна, що відповідає заповненню електронами валентної зони, починаючи з найбільш низьких її рівнів. При підвищенні температури енергія теплового руху електронів зростає і вони стають здатними займати більш високі енергетичні рівні.
Якщо створити вкристалі електричне поле, то воно може спричинити скероване переміщення цих електронів (електрострум провідності). Однак це можливо лише в таких кристалах, де є більш високі енергетичні рівні, які можуть бути заповненими електронами. Сукупність таких рівнів називається зоною провідності.
В металічних кристалах кількість валентних електронів менша від кількості енергетичних рівнів, на які ці електрони можуть переходити. Наприклад, у одновалентних металів валентна зона заповнена наполовину, а незаповнена її частина є зоною провідності (рис. 3).
 |
Рис. 3.
У двовалентних металів валентна зона заповнена повністю, проте верхня її зона виявляється розташованою вище від нижньої границі наступної зони дозволених енергій (рис. 4), тобто ці зони частково перекриваються і область перекриття стає зоною провідності. Такі кристали є провідниками електричного струму.
 |
Рис. 4.
Температурна залежність електропровідності будь-якого матеріалу визначається залежністю від температури концентрації носіїв струму та їхньою рухливістю. В металах концентрація електронів провідності незмінна, а рухливість електронів з підвищенням температури зменшується, отже зменшується провідність і збільшується опір кристалів.
Класична теорія провідності металів грунтується на тому, що вільні електрони (електронний газ) поводять себе так, як молекули ідеального газу. Вони рухаються зі швидкістю 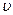 , співударяються переважно зіонами гратки, пробігаючи між зіткненнями відстань
, співударяються переважно зіонами гратки, пробігаючи між зіткненнями відстань 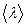 , яка називається середньою довжиною вільного пробігу і дорівнює значенню міжатомної відстані в кристалі. На основі цих уявлень, можна отримати наступний вираз для питомої електропровідності металів:
, яка називається середньою довжиною вільного пробігу і дорівнює значенню міжатомної відстані в кристалі. На основі цих уявлень, можна отримати наступний вираз для питомої електропровідності металів:
 (1)
(1)
де n- концентрація електронів, е- заряд електрона, m- маса електрона.
В цьому виразі величини n, m, е, λ- сталі, а 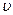 прямопропорційна до
прямопропорційна до  , де Т- температура. Таким чином, за класичною теорією питома електропровідність залежить від природи металу і обернено пропорційна
, де Т- температура. Таким чином, за класичною теорією питома електропровідність залежить від природи металу і обернено пропорційна  .
.
Однак, досліди показують, що в широкому інтервалі температур опір металів прямопропорційний до Т (рис. 5).
 |
Рис. 5.
В інтервалі середніх і високих температур опір металів збільшується при зростанні температури за лінійним законом
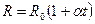 , (2)
, (2)
де R і R0 - опір при температурах t°С і 0° С відповідно, α- температурний коефіцієнт опору (ТКО), який визначається експериментально.
За величиною ТКО:
 , (3)
, (3)
тобто фізичний зміст ТКО полягає у відносній зміну кожної початкової одиниці опору при зміні температури на один градус. Вимірюється ТКО в град-1.
За низьких температур для багатьох металів залежність R = f(T) має інший характер (рис. 6). Тобто при певній для даного металу низькій температурі Тк, яка називається критичною, опір падає практично до нуля. Це явище називається надпровідністю, в межах класичної теорії воно не пояснюється.
Причиною розходжень результатів класичної теорії з експериментальними фактами є те, що в цій теорії не враховуються квантові властивості електронів. З врахуванням цих властивостей виходить, що у виразі (1) величина 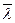 є аналогічна середній довжині вільного пробігу електронів у металі і залежить обернено пропорційно від Т.
є аналогічна середній довжині вільного пробігу електронів у металі і залежить обернено пропорційно від Т.
Величина 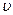 являє собою швидкість електронів у валентній зоні і практично не залежить від Т. Таким чином, провідність металів обернено пропорційна, а опір прямопропорційний температурі Т.
являє собою швидкість електронів у валентній зоні і практично не залежить від Т. Таким чином, провідність металів обернено пропорційна, а опір прямопропорційний температурі Т.
Явище надпровідності пояснюється обмінною взаємодією між електронами і має квантову природу.
 |
Рис. 6.
Метод вимірювань.
Метод вимірювань полягає у визначенні опору метала при різних температурах. Якщо побудувати графік залежності R = f(t°), то шляхом екстраполяції можна знайти опір метала R0 при 0° С. Тангенс кута нахилу прямої R = f(t,°С) визначається виразом
 (4)
(4)
і співпадає з величиною  в формулі (2). Отже, ТКО визначається виразом:
в формулі (2). Отже, ТКО визначається виразом:
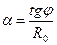 (5)
(5)
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |