
Динаміка собівартості озимої пшениці та соняшнику
|
|
В даному розділі розглянемо показники рядів динаміки, згладжування ряду динаміки за допомогою ковзної середньої, а також аналітичне вирівнювання по прямій і по параболі другого порядку. Так як в даному розділі розглядаємо дві культури, то спочатку все вказане вище опишемо для озимої пшениці, а потім для соняшника.
Усі природні та суспільні явища находяться в постійному розвитку. Процеси розвитку явищ у часі називають динамікою, а статистичні показники, які характеризують стан і зміну у часі, - рядами динаміки.
Елементами ряду динаміки є моменти, або періоди, часу (день, місяць, рік і т. д.), до яких належать досліджувані показники і рівні ряду, які характеризують розмір явища.
Під час аналізу динаміки суспільно-економічних явищ визначають такі показники як: абсолютний приріст, темпи зростання і приросту, абсолютне значення 1% приросту на основі порівняння рівнів ряду динаміки. Рівень, який порівнюють, називається поточним, а рівень, з яким порівнюють, – базисним.
Абсолютний приріст визначають як різницю між поточним і попереднім, або початковим рівнями ряду динаміки. Цей показник показує, на скільки одиниць підвищився або зменшився поточний рівень порівняно з базисним за відповідний період часу.
Якщо порівнюють кожний рівень ряду динаміки з попереднім рівнем, то абсолютний приріст буде ланцюговим. Якщо всі рівні ряду порівнюють з початковим, який є постійною базою порівняння, то такий абсолютний приріст буде базисним.
Темп зростання – це відношення поточного рівня ряду динаміки до попереднього, або початкового, рівня.
Темп зростання може бути ланцюговим, коли порівнюють поточний рівень з попереднім, і базисним, коли порівнюють поточний рівень з початковим.
Темп приросту показує, на скільки процентів збільшився або зменшився поточний рівень ряду динаміки порівняно з базисним. Його обчислюють як відношення абсолютного приросту до попереднього або початкового рівня. Цей показник можна також визначити, віднімаючи від темпу зростання, вираженого в процентах, 100.
Абсолютне значення 1% приросту дорівнює відношенню абсолютного приросту за певний період до темпу приросту за той самий період.
Таблиця 3.2.
Динаміка собівартості 1ц озимої пшениці в ТОВ “Зернопродукт”
| Роки | Собівартість, грн | Абсолютний приріст, грн | Темп зростання, % | Темп приросту, % | Абсолютне зна-чення 1% при-росту | |||
| Ланцюговий | Базисний | Ланцюговий | Базисний | Ланцюговий | Базисний | |||
| 28,52 | --- | --- | --- | --- | --- | --- | ||
| 39,46 | 10,94 | 10,94 | 138,36 | 138,36 | 38,36 | 38,36 | 0,28 | |
| 52,44 | 12,98 | 23,92 | 132,89 | 183,87 | 32,89 | 83,87 | 0,39 | |
| 45,43 | -7,01 | 16,91 | 86,63 | 159,29 | -13,37 | 59,29 | 0,52 | |
| 16,4 | -29,03 | -12,12 | 36,1 | 57,5 | -63,9 | -42,5 | 0,45 |
Дані таблиці показують, що у 2011 році собівартість найменша. Абсолютний приріст собівартості найбільший у 2009 році як ланцюговий, так і базисний. Це каже про те, що в цьому році було вкладено дуже багато затрат на вирощування 1 ц озимої пшениці. Але якщо подивиться на темп зростання та приросту собівартості, тобто на темп зростання та приросту витрат, то видно, що він найбільший у 2008 році, так як собівартість у 2008 році збільшилась на 138,36% і 38,36% відповідно – це при ланцюговому темпові зростання, але при базисному темпі зростання він найбільший у 2009 році, тому що собівартість у 2009 році збільшилась на 183,87% і 83,87% відповідно. Абсолютне значення 1% приросту збільшилось з 0,28 грн у 2008 році до 0,52 грн у 2010 році.
Закономірності розвитку в рядах динаміки визначають абстрагуванням від випадкових змін досліджуваних ознак. Для цього статистика використовує один із способів такий як спосіб ковзної середньої. Суть згладжування ряду динаміки за допомогою ковзної середньої полягає в тому, що при стійкому інтервалі кожну наступну середню обчислюють, зсуваючи період на одну дату.
Визначаючи ковзну середню, спочатку додають рівні ряду за прийнятий інтервал часу і обчислюють середню арифметичну. Після цього утворюють новий інтервал, починаючи з другого рівня ряду, для якого визначають нову середню і т. д.
Таблиця 3.3.
Тенденція зміни динаміки собівартості 1ц озимої пшениці в ТОВ “Зернопродукт” методом трьохрічної ковзної
| Роки | Собівартість, грн | Період | Сума трьохрічної ковзної | Сума середньої трьохрічної ковзної |
| 28,52 | ------ | ---- | ---- | |
| 39,46 | 2007 – 2009 | 120,42 | 40,14 | |
| 52,44 | 2008 – 2010 | 137,33 | 45,78 | |
| 45,43 | 2009 – 2011 | 114,27 | 38,09 | |
| 16,4 | ------ | ---- | ---- |
Спосіб середньої ковзної згладжує коливання рівнів, але не дає рядів, які б замінювали всі вихідні фактичні рівні вирівняними.
Найбільш досконалим способом виявлення закономірностей є аналітичне вирівнювання способом найменших квадратів. Вирівнювання способом найменших квадратів можна здійснити по прямій і по параболі другого порядку, яка виражає функціональну залежність рівнів ряду динаміки від часу.
Для вирівнювання по прямій необхідна пряма лінія, рівняння якої має такий вигляд :
ỹt = a0+а1t,(3.1)
де ỹt – вирівняні рівні ряду динаміки,
а0 – вирівняний рівень собівартості,
а1 – середній щорічний приріст (або зниження) собівартості,
t – порядковий номер року.
Невідомі параметри а і а знаходять способом найменших квадратів, розв’язуючи систему нормальних рівнянь (2.2):
∑y = na0+ a1∑t; (3.2)
∑yt = a0∑t +a1∑t,
де y – фактичні рівні ряду динаміки (в нашому прикладі фактична собівартість),
n – кількість років у періоді, що вивчається.
Методику вирівнювання ряду динаміки розглянемо за даними про собівартість озимої пшениці. Потрібні дані для розв’язання системи рівнянь знаходяться нижче у таблиці 2.4.
Переносимо підсумкові дані в систему рівнянь:
182,25 = 5a0,
-18,27 = 10а1.
Звідси а0= 36,45, а1= -1,83.
Отже, рівняння прямої лінії, яке характеризує динаміку собівартості озимої пшениці, матиме такий вигляд:
ỹt = 36,45 – 1,83t.
Це означає, що в 2006 році, тобто в році, який передує досліджуваному періоду, вирівняна собівартість 1ц озимої пшениці становила 36,45 грн, а середня собівартість щорічно зменшується на 1,83 грн.
Підставляючи в отримане рівняння по черзі значення t, дістанемо вирівняний (теоретичний) динамічний ряд собівартості озимої пшениці:
ỹt1999= 36,45 – 1,83(-2) = 40,11,
ỹt2000=36,45 – 1,83(-1) = 38,28,
ỹt2001=36,45 – 1,83*0 = 36,45,
ỹt2002=36,45 – 1,83*1 = 34,62,
ỹt2003=36,45 – 1,83*2 = 32,79.
Вирівняні значення рівнів ряду динаміки наведено в табл.3.4 .
Таблиця 3.4.
Вихідні дані для вирівнювання ряду динаміки собівартості озимої пшениці по прямій і по параболі другого порядку
| Роки | Фактична со-бівар-тість, грн | Номер року | Розрахункові величини | Вирівняне значення по прямій | Вирівняне значення по параболі | ||||
| y | T | t2 | t3 | t4 | Yt | yt2 | ỹt | ỹt’ | |
| 28,52 | -2 | -8 | -57,04 | 114,08 | 40,11 | 25,83 | |||
| 39,46 | -1 | -1 | -39,46 | 39,46 | 38,28 | 45,42 | |||
| 52,44 | 36,45 | 50,73 | |||||||
| 45,43 | 45,43 | 45,43 | 34,62 | 41,76 | |||||
| 16,4 | 32,8 | 65,6 | 32,79 | 18,51 | |||||
| ∑ | 182,25 | -18,27 | 264,57 | 182,25 | 182,25 |
Для вирівнювання рядів динаміки по параболі другого порядку необхідно рівняння (2.3):
ỹt’ = a0+a1t+a2t2, (3.3)
де ỹt – вирівняні рівні ряду динаміки,
а0 – вирівняний рівень собівартості,
а1 – середній щорічний приріст ( або зниження) рівня,
а2 – середнє прискорення або сповільнення зростання ( зниження) рівня досліджуваного явища,
t – порядковий номер дат.
Невідомі параметри а , а , а знаходять розв’язанням системи рівнянь (3.4):
∑y = na0+a1∑t +a2∑t,
∑yt = a0∑t +a1∑t2+a2∑t3, (3.4)
∑yt = a0∑t2+a1∑t3+a2∑t4,
де y - фактичні рівні ряду динаміки,
n - кількість дат.
Переносимо дані з табл. 3.4 у систему рівнянь з трьома невідомими параметрами:
182,25 = 5а0+10а2 ,
-18,27 = 10а1,
264,57 = 10а0+34а2 .
Звідси а1= -1,83, а невідомі параметри а0 і а2 знаходимо з наступної системи рівнянь:
182,25 = 5а0+10а2,
264,57 = 10а0+34а2.
Розв’язав дану систему, отримуємо значення параметру а2= -7,14, а значення параметру а знаходимо підставляючи значення а в перше рівняння даної системи, тоді а0= 50,73.
Це означає, що в 2006 р., який передує досліджуваному періоду, вирівняна собівартість озимої пшениці становила 50,73 грн, середнє абсолютне зниження рівня собівартості складає – 1,83, середнє прискорення зниження рівня собівартості озимої пшениці складає –7,14.
Підставляючи в рівняння ỹt = 50,73 –1,83t – 7,14t2 по черзі значення для відповідного року, дістанемо вирівняні (теоретичні) значення рівнів собівартості озимої пшениці:
ỹt’1999 =50,73 – 1,83(-2) – 7,1484 = 25,83,
ỹt’2000 =50,73 – 1,83(-1) – 7,14*1 = 45,42,
ỹt’2001 =50,73 – 1,83*0 – 7,14*0 = 50,73,
ỹt’2002= 50,73 – 1,83*1 – 7,14*1 = 41,76,
ỹt’2003= 50,73 – 1,83*2 – 7,14*4 = 18,51.
Розрахунки по параболі показали, що абсолютний приріст собівартості озимої пшениці значно відрізняються один від одного. Існує тенденція як стрімкого зростання показника у 2007-2009 роках, так і стрімкого спаду у 2010 і 2011 р.р.
Для того, щоб прослідити тенденції зміни собівартості озимої пшениці більш наочно розглянемо на рис. 3.1, який зображено нижче.

Рисунок 3.1. Зміна собівартості озимої пшениці в цілому, по прямій і по параболі
Для узагальнюючої характеристики динаміки собівартості розраховується:
Середній абсолютний приріст – показує, на скільки одиниць в середньому щорічно підвищувались (зменшувались) рівні ряду динаміки:

 ,(3.5)
,(3.5)
де  Y – середній абсолютний приріст;
Y – середній абсолютний приріст;
 Yл – ланцюгові абсолютні прирости;
Yл – ланцюгові абсолютні прирости;
m – кількість ланцюгових абсолютних приростів;
Yn - останній рівень ряду динаміки;
Y0 - базисний рівень ряду динаміки;
n – кількість рівнів ряду динаміки.
Середній темп приросту (у відсотках) – показує, скільки в середньому відсотків складає кожний поточний рівень від попереднього. Для розрахунку використовується формула середньої геометричної; в підкореневому виразі темпи росту доцільно представляти в коефіцієнтах:
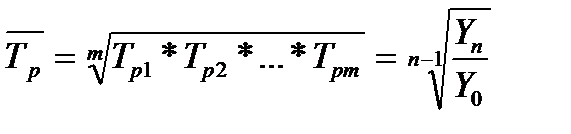 , (3.6)
, (3.6)
де 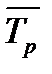 - середній темп приросту;
- середній темп приросту;
m – кількість ланцюгових темпів приросту;
Tp1…m- темпи росту ланцюгові ( у коефіцієнтах);
Yn – останній рівень ряду динаміки;
Y0 – базисний рівень ряду динаміки.
Середній темп приросту – показує, на скільки відсотків в середньому збільшувався (зменшувався) кожний поточний рівень ряду порівняно з попереднім:
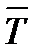
 (3.7)
(3.7)
де  - середній темп приросту;
- середній темп приросту;
 - середній темп росту (у відсотках).
- середній темп росту (у відсотках).
Середнє абсолютне значення 1% приросту – показує середню інтенсивність збільшення (якщо середній абсолютний прирост додатній) або зменшення (якщо середній абсолютний приріст від ємний) рівнів ряду динаміки:
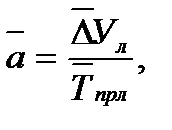 (3.8)
(3.8)
де 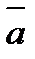 - середнє абсолютне значення 1% приросту;
- середнє абсолютне значення 1% приросту;
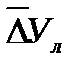 - середній абсолютний приріст;
- середній абсолютний приріст;
 - середній темп приросту.
- середній темп приросту.
Підставивши дані по собівартості озимої пшениці у вищенаведені формули, отримуємо, що: середній абсолютний приріст дорівнює –3,03 (це каже про те, що собівартість в середньому щорічно зменшувалась на 3,03грн);середній темп росту – 87% ( це вказує на те, що в середньому 87% складає кожний поточний рівень від попереднього); середній темп приросту дорівнює -13% (це показує, що в середньому на 13% зменшувався кожний поточний рівень собівартості порівняно з попереднім); середнє абсолютне значення 1% приросту – 0,23 ( 0,23 – це середня інтенсивність збільшення собівартості).
Так як закінчили описання показників ряду динаміки, згладжування ряду динаміки за допомогою ковзної середньої та аналітичне вирівнювання рядів динаміки способом найменших квадратів, тобто по прямій і по параболі, для собівартості озимої пшениці, то переходимо до описання вище сказаного для собівартості соняшнику.
Таблиця 3.5.
Динаміка собівартості 1ц соняшника в ЗАТ “Зернопродукт”
| Роки | Собівартість, грн. | Абсолютний приріст, грн | Темп зростання, % | Темп приросту, % | Абсолют-не значен-ня 1% приросту | |||||
| Ланцюговий | Базисний | Ланцюговий | Базисний | Ланцюговий | Базисний | |||||
| 28,64 | --- | --- | --- | --- | --- | --- | ||||
| 41,46 | 12,82 | 12,82 | 144,76 | 144,76 | 44,76 | 44,76 | 0,28 | |||
| 55,43 | 13,97 | 26,82 | 133,69 | 193,54 | 33,69 | 93,54 | 0,41 | |||
| 40,27 | -15,16 | 11,63 | 72,65 | 140,61 | -27,35 | 40,61 | 0,55 | |||
| 21,53 | -18,74 | -7,11 | 53,46 | 75,17 | -46,54 | -24,83 | 0,4 | |||
Дані табл.3.5 показують, що за 2007 – 2011 р.р. собівартість соняшника у 2003 році найменша. Абсолютне значення 1% приросту збільшилось з 0,28 грн у 2000 р. до 0,55 грн у 2010 р. Абсолютний приріст собівартості як ланцюговий, так і базисний у 2009 р. найбільший. Ланцюговий темп зростання і приросту собівартості у 2008 році найбільший і складає 144,76% і 44,76% відповідно, а базисний темп зростання і приросту найбільший у 2009 році. Всі вище перераховані показники найбільші як для озимої пшениці, так і для соняшника в однакових роках. Це каже про те, що в даних роках господарство понесло значні витрати для вирощування цих культур.
Розглянемо зміну собівартості 1ц соняшнику способом середньої ковзної, що наведена в табл.3.6.
Таблиця 3.6
Тенденція зміни динаміки собівартості 1ц соняшнику в ЗАТ “Зернопродукт” методом трьохрічної ковзної
| Роки | Собівартість, грн. | Період | Сума трьохрічної ковзної | Сума середньої трьохрічної ковзної |
| 28,64 | ------ | ---- | ---- | |
| 41,46 | 2007 –2009 | 125,53 | 41,84 | |
| 55,43 | 2008 – 2010 | 137,16 | 12,39 | |
| 40,27 | 2009 – 2011 | 117,23 | 39,08 | |
| 21,53 | ------ | ---- | ---- |
Так як спосіб ковзної середньої є недоцільним, тому що не дає рядів, які б замінювали всі вихідні фактичні рівні вирівняними, тому розглянемо вирівнювання собівартості 1ц соняшника по прямій і по параболі другого порядку. Для цього необхідно заповнити наступну таблицю 3.7, що розташована нижче.
Робимо вирівнювання по прямій, вигляд якої вже був вказаний вище, тому невідомі показники а0 і а1 знаходимо розв’язуючи систему рівнянь, загальний вигляд якої вже був показаний вище, і тому переносимо дані з табл.2.6 в систему рівнянь і маємо:
187,33 = 5а0,
-15,41 = 10а1.
Звідси показники а0= 37,47 і а1= -1,54.
Таблиця 3.7
Вихідні дані для вирівнювання ряду динаміки собівартості 1ц соняшнику по прямій і по параболі другого порядку
| Роки | Собівартість, грн. | Номер року | Розрахункові величини | Вирівняне значення по прямій | Вирівняне значення по параболі | ||||
| Y | T | T2 | t3 | t4 | yt | yt2 | ỹt | ỹt’ | |
| 28,64 | -2 | -8 | -57,28 | 114,56 | 40,55 | 27,37 | |||
| 41,46 | -1 | -1 | -41,46 | 41,46 | 39,01 | 45,6 | |||
| 55,43 | 37,47 | 50,65 | |||||||
| 40,27 | 40,27 | 40,27 | 35,93 | 42,52 | |||||
| 21,53 | 43,06 | 86,12 | 34,39 | 21,21 | |||||
| ∑ | 187,33 | -15,41 | 282,41 | 187,35 | 187,35 |
Отже, рівняння прямої лінії, яке характеризує динаміку собівартості соняшнику матиме такий вигляд:
ỹt = 37,47 – 1,54t (3.9)
Це означає, що в 2009 році, тобто в році, який передує досліджуваному, вирівняна собівартість соняшнику становила 37,47 грн, а середнє щорічне зниження собівартості дорівнює 1,54 грн.
Підставляємо по черзі в рівняння, наведене вище, по черзі t, дістанемо вирівняний ( теоретичний) динамічний ряд собівартості соняшнику:
ỹt1999= 37,47 –1,54(-2) = 40,55,
ỹt2000= 37,47 – 1,54(-1) = 39,01,
ỹt2001= 37,47 – 1,54*0 = 37,47,
ỹt2002= 37,47 – 1,54*1 = 35,93,
ỹt2003= 34,39 – 1,54*2 = 34,39.
Далі як і по озимій пшениці розглядаємо вирівнювання собівартості соняшнику за рівнянням параболи, яке вже було наведене вище, тому знаходимо невідомі параметри а0, а1, а2 розв’язанням системи рівнянь, загальний вигляд якої наведений вище, і тому маємо таку систему рівнянь:
187,33 = 5а0+10а2,
-15,41 = 10а1,
282,41 = 10а0+34а2 .
Розв’язав цю систему рівнянь, бачимо, що показники а0= 50,65, а1= -1,45, а2= -6,59.
Отже, рівняння параболи другого порядку, яке характеризує динаміку собівартості соняшнику, матиме вигляд:
ỹt’= 50,65 – 1,54t – 6,59t2.
Це означає, що в 2006 р., тобто в році, який передує досліджуваному періоду, вирівняна собівартість соняшнику становила 50,65 грн, середнє абсолютне зниження рівня собівартості дорівнює –1,54 грн, а середнє прискорення зниження рівня собівартості соняшника складає –6,59.
Підставляючи в дане рівняння по черзі значення для відповідного року, дістанемо вирвняні ( теоретичні) рівні собівартості соняшнику:
ỹt’1999= 50,65 – 1,54(-2) – 6,59*4 = 27,37,
ỹt 2000 = 50,65 – 1,54(-1) – 6,59*1 = 45,6,
ỹt’2001= 50,65 – 1,54*0 – 6,59*0 = 50,65,
ỹt’2002= 50,65 – 1,54*1 – 6,59*1 = 42,52,
ỹt’2003= 50,65 – 1,54*4 – 6,59*4 = 21,21.
Розрахунки показали, що абсолютний приріст собівартості соняшнику, як і озимої пшениці, значно відрізняються один від одного. Також існує тенденція як стрімкого зростання показника у 2007-2009 рр., так і стрімкого спаду у 2010 і 2011 роках.
Для узагальнюючої характеристики динаміки собівартості розрахуємо також середній абсолютний приріст, середній темп росту, середній темп приросту, середнє абсолютне значення 1% приросту. Підставивши дані по собівартості соняшнику у формули для розрахунку цих показників, які були наведені вище, отримуємо, що: середній абсолютний приріст дорівнює –1,78 (це каже про те, що собівартість в середньому щорічно зменшувалась на 1,78грн);середній темп росту – 93% ( це вказує на те, що в середньому 93% складає кожний поточний рівень від попереднього); середній темп приросту дорівнює -7% (це показує, що в середньому на 7% зменшувався кожний поточний рівень собівартості порівняно з попереднім); середнє абсолютне значення 1% приросту – 0,25 ( 0,25 – це середня інтенсивність збільшення собівартості).
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |