
Лекція № 3. Лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами..
|
|
Мета: Узагальнити та систематизувати знання студентів про диференціальні рівняння другого порядку зі сталими коефіцієнтами.
Сформувати вміння розв’язувати задачі, що передбачають використання диференціальних рівнянь, використання поняття інтегралів.
План
1. Диференціальні рівняння другого порядку.
2. Приклади.
Домашне завдання: Індивідуальні завдання.
 Лінійним диференціальним рівнянням другого порядку з постійними коефіцієнтами називається рівняння виду
Лінійним диференціальним рівнянням другого порядку з постійними коефіцієнтами називається рівняння виду
y|| + py| + qy = f(x), де р и q – деякі числа. 
Якщо f(x) = 0, то диференціальне рівняння називається
лінійним однорідним. Воно має вид y|| + py| + qy = 0. (1)
Рішенням даного диференціального рівняння повинна бути така функція, що, будучи підставлена в рівняння, перетворитися в тотожність. Ліва частина рівняння являє собою суму функції в і її похідних y| і y||, узятих з деякими постійними коефіцієнтами. Щоб така сума звернулася в нуль, треба, щоб у, y| і y|| були подібні між собою.
Такою функцією є функція у = екх. Потрібно підібрати так, щоб ця функція задовольняла рівнянню.
Тому що: 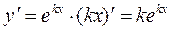 ,
,
 ,
,
 та представляючи ці значення в, y| і y|| у ліву частину рівняння, одержимо:
та представляючи ці значення в, y| і y|| у ліву частину рівняння, одержимо: 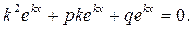
Скорочуючи на множник 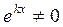 , одержимо характеристичне рівняння:
, одержимо характеристичне рівняння: 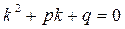
Рівняння визначає ті значення , при який функція у = екх є рішенням диференціального рівняння (1).
При рішенні характеристичного рівняння можливі три випадки, у залежності від який будується загальне рішення даного диференціального рівняння (1):
| Корені рівняння k2 + pk + q = 0 | Часні рішення рівняння y|| + py| + qy = 0. | Загальне рішення рівняння y|| + py| + qy = 0. |
Дійсні і різні 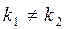
| y1 = ek1x y2 = ek2x | y = c1ek1x + c2ek2x |
Рівні: 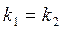
| y1 = ek1x y2 = xek2x | y = ek1x (1 + c2x) |
Комплексно – сполучені 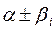
| y1 = 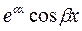 y1 =
y1 = 
| y = 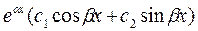
|
Розв’язування прикладів.
Приклад 1. Знайти загальне рішення диференціального рівняння:
y|| –5y| + 6y = 0.
Розв’язання. Складемо характеристичне рівняння і знайдемо його корені:
k2 – 5k + 6 = 0 (y|| = k2; y| = k; y = 1.)
D = 25 – 24 = 1
k1,2 = 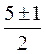 = 2; 3.
= 2; 3.
Корені характеристичного рівняння є дійсними і різними. Тому:
y1 = e2x; y2 = e3x – часні розв’язки;
y = c1e2x + c2e3x – загальне рішення даного диф. рівняння.
Приклад 2. Знайти загальне рішення диференціального рівняння:
y|| +4y| +4y = 0.
Розв’язання: Характеристичне рівняння:
k2 + 4k + 4 = 0; (y|| = k2; y| = k; y = 1)
(k + 2)2 = 0 має дійсні рівні корені k1 = k2 = –2.
Тому: y1 = e-2x, y2 = xe-2x – часні розв’язки.
y = c1e-2x + c2e-2xx = e-2x(c1 + xc2) – загальне рішення даного
дифрівняння.
Приклад 3. Знайти загальне рішення диференціального рівняння:
y|| +6y| +13y = 0.
Розв’язання: Характеристичне рівняння:
k2 + 6k + 13 = 0; (y|| = k2; y| = k; y = 1),
D = 36 – 52 = – 16,
має корені: k1,2 = 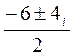 ;
;
k1 = – 3 + 2і; k2 = – 3 – 2і.
Корені рівняння є комплексно – сполученими. Тому:
y1 = e-3xcos2x,
y2 = e-3xsin2x - часні розв’язки.
y = c1e-3x (c1cos2x + c2sin2x) – загальне рішення диф. рівняння
Приклад 4. Знайти приватне рішення диференціального рівняння
y|| – 2y| + y = 0, що задовольняє початковим умовам
при х = 0, у = 4, y| = 2.
Розв’язання: Характеристичне рівняння:
k2 – 2k + 1 = 0 чи (k–1)2 = 0 має дійсні рівні корені k1 = k2 = 1, тому:у1 = ех, у2 = хех – часні розв’язки диф. рівняння
у = ех (з1 + з2) – загальне рішення диф. рівняння.
Для визначення приватного рішення, що задовольняє даним початковим умовам, спочатку знайдемо похідну:
y| для функції в = ех (з1+з2):
y| = (ех(з1+з2х))| = е (з1+з2х) + ехс2 = ех(з1+з2+з2х)
Тепер підставимо початкові умови у вираження в і у| :
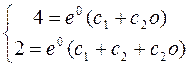 ,
, 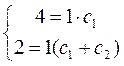 ,
, 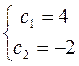
Підставивши ці значення в загальне рішення знайдемо приватне рішення диф. рівняння, що задовольняє даним початковим умовам:
у = ех(4 – 2х)
Відповідь: у = ех(4 – 2х).
Приклад 5. Знайти загальне рішення диференціального рівняння:
y|| + y| – 2y = 0
Розв’язання:
k2 + k – 2 = 0 – характеристичне рівняння.
k1 = –2; k2 = 1 – корені.
y1 = e-2x, y2 = ex – загальне рішення диф. рівняння.
Приклад 6. Знайти загальне рішення диференціального рівняння:
y|| – 6y| + 9 = 0
Розв’язання:
k2 – 6k + 9 = 0 – характеристичне рівняння.
(k – 3)2 = 0
k1 = 3; k2 = 3 – корені.
y1 = e3x, y2 = xe3x – часні рішення диф. рівняння.
y = С1e3x + С2xe3x = e3x(С1 + С2x) – загальне рішення.
Приклад 7. Знайти приватне рішення рівняння y|| + 2y| + 6у = 0, що задовольняє початковим умовам при х = 0, у = 0, y| = 1.
Розв’язання:
k2 + 2k + 5 = 0
D = 4 – 20 = –16, k1,2 = 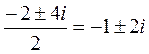 .
.
y1 = e-xcos2x, y2 = e-xsin2x – часне рішення.
у = e-x (С1cos2x + С2sin2x) – загальне рішення.
Знайдемо часне рішення задовольняюче початковим умовам.
0 = е0(С1cos0 + С2sin0),
0 = 1 (С1 1 + С2 0),
c1 = 0.
Знайдемо y| = (e-x(С1cos2x + С2cos2x))| =
= - e-x(С1cos2x + С2sin2x) + e-x(-2С1sin2x + 2С2cos2x) =
= e-x(-С1cos2x – С2sin2x – 2С1sin2x + 2С2cos2x);
С1 = 0, то y| = е-х(2С2cos2x – С2sin2x)
x = 0, y| = 1, те 1 = e0(2С2cos0 – С2sin0)
1 = 1(С2 – 0)
1 = 2С2, С2 = 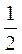 .
.
Отже:
y = e-x(0cos2x + 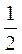 sin2x)
sin2x)
y = e-x 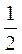 sin2x
sin2x
y = 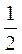 e-xsin2x – часне рішення.
e-xsin2x – часне рішення.
Приклад 8. Знайти інтегральну криву диференціального рівняння
y|| + 2y| + 2у = 0, що проходить через крапку М (0;1) і, що дотикається в цій точці прямої у = х + 1.
Розв’язання
Характеристичне рівняння має вид:
k2 + 2k + 2 = 0
D = 4 – 8 = –4
k1,2 = 
y1 = e-xcosx, y2 = e-xsinx – часне рішення.
y = e-x(С1cosx + С2sinx) – загальне рішення.
Знайдемо y| = – e-x (-С1cosx – С2sinx – С1sinx + С2cosx)
y| = – e-x ((С2 – С1)cosx – (С2 + С1)sinx).
Знайдемо рівняння шуканої інтегральної кривої, для чого в рівності підставимо значення в = 1 і кутового коефіцієнта
y| = k = 1 у точці х = 0.
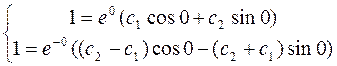
 ,
, 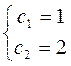
у = e-x (cosx + 2sinx) – інтегральна крива диф. рівняння, що проходить через точку М(0;1) і, що дотикається в цій точці прямої у = х + 1.
Приклад 9. Вирішити рівняння: y|| – 7y| + 10у = 0
Розв’язання
k2 – 7k + 10 = 0 – характеристичне рівняння.
(k – 5) (k – 2) = 0
k = 5, k = 2 – корені.
y1 = e5x, y2 = e2x – часні рішення
y = c1e5x + c2e2x – загальне рішення.
Приклад 10. Знайти часне рішення рівняння:
y|| – 5y| = 0, якщо при х = 0, у = 1, y| = –1.
Розв’язання
k2 – 5k = 0 – характеристичне рівняння.
k(k – 5) = 0
k = 0, k = 5 – корені характеристичного рівняння.
у1 = у0х = 1, у2 = е5х – часні рішення.
у = з1 1 + з2е5х; у = з1 + з2е5х – загальне рішення.
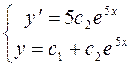
 ,
, 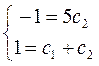 ,
, 
Шукане часне рішення має вид:

Приклад 11. Знайти приватне рішення рівняння:
y|| + 8y| + 16у= 0, якщо при х = 0, у = 1, y| = 1.
Розв’язання
k2 – 8k + 16= 0 – характеристичне рівняння.
D = 64 – 64 = 0.
k1,2 = – 4.
y1 = e-4x, y2 = xe-4x – часне рішення.
y = e-4x(c1 + c2) – загальне рішення.
y| = – 4е-4х(с1 + с2х) + е-4хс2 = е-4х(–4с1–4с2х + с2)
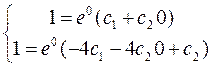 ,
, 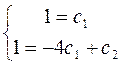 ,
, 
Шукане часне рішення має вид:
у = е-4х(1+5х).
Приклад 12. Вирішити рівняння y|| – 6y| + 25у= 0
Розв’язання
Характеристичне рівняння:
k2 – 6k + 16= 0
D = 36 – 100 = – 64
k1,2 = 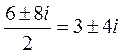
y1 = e3xcos4x, y2 = e3xsin4x – часне рішення.
y = e3x(c1cos4x + c2sin4x) – загальне рішення.
Приклад 13. Знайти приватне рішення рівняння y|| – 6y| + 13у= 0,
якщо х = 0, у = 1, y| = 5.
Розв’язання
Характеристичне рівняння:
k2 – 6k + 13= 0
D = 36 – 52 = – 16
k1,2 = 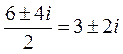
y1 = e3xcos2x, y2 = e3xsin2x – часне рішення
y = e3x(С1cos2x + С2sin2x) – загальне рішення.
y| = 3e3x(С1cos2x + С2sin2x) + e3x(–2С1sin2x + 2С2cos2x)=
y| = e3x(3С1cos2x + 3С2sin2x – 2С1sin2x + 2С2cos2x).
y| = e3x((3С1 + 2С2)cos2x + (3С2 – 2С1)sin2x).
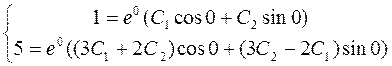
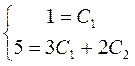 ,
, 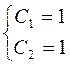
Шукане часне рішення має вид: y = e3x(cos2x + sin2x).
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |