
Векторний добуток двох векторів в координатній формі
|
|
Нехай в прямокутній системі координат задані вектори  і
і  . Доведемо, що векторний добуток вектора
. Доведемо, що векторний добуток вектора 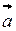 на вектор
на вектор 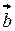 визначається формулою
визначається формулою
 . (1.23)
. (1.23)
Доказ. Використовуючи властивості 1 – 3 і 6 векторних добутків і теорему про розкладання визначника, маємо
 =
=
 +
+  +
+  +
+  +
+  +
+
+  +
+  +
+ 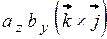 +
+  =
=
= 
 +
+  +
+ 
 =
=
= 
 +
+  =
=

 +
+ 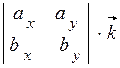 =
=  .
.
 Геометричний зміст векторного добутку.
Геометричний зміст векторного добутку.
Модуль векторного добутку рівний площі паралелограма, побудованого на цих векторах, як на сторонах:
|
 .
.
Механічне зміст векторного добутку.

|
Момент сили  , прикладеної
, прикладеної
до точки А відносно точки  ,
,
рівний векторному добутку
сили  на вектор
на вектор  :
:
 .
.
Приклад 3.Обчислити площу паралелограма побудованого на векторах
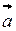 і
і 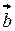 , якщо:
, якщо:
а)  ;
;  ;
;  ;
;  ;
; 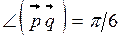 ;
;
б)  ;
;  .
.
Розв’язок.Площа паралелограма, побудованого на векторах 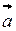 і
і 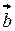 , згідно формули (1.22) дорівнює модулю їх векторного добутку
, згідно формули (1.22) дорівнює модулю їх векторного добутку
 .
.
Знайдемо векторний добуток векторів 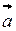 і
і 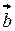
а) 

 .
.
Тобто площа паралелограма


 (кв. од.).
(кв. од.).
Відповідь: 7 кв. од.
б) Якщо вектора задані своїми проекціями на осі координат, то в цьому випадку їх векторний добуток обчислюється по формулі (2.23)
 .
.
У нашому випадку


Площа паралелограма в цьому випадку
 (кв. од.)
(кв. од.)
Відповідь.  кв. од.
кв. од.
Змішаний добуток трьох векторів
Визначення і обчислення змішаного добутку
Змішаним добутком трьох векторів 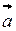 ,
, 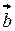 і
і  називається число, що є добутком вектора
називається число, що є добутком вектора  скалярно на вектор
скалярно на вектор  :
:
 . (1.24)
. (1.24)
Тут перші два вектори перемножуються один на одного векторно, а потім отриманий вектор  множиться скалярний на третій вектор.
множиться скалярний на третій вектор.
Знайдемо вираз для змішаного добуток через координати векторів, що перемножуються. Визначимо спочатку  :
:
 =
= 
 +
+ 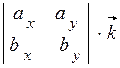
Оскільки  , то по формулі (1.17)
, то по формулі (1.17)
 ,
,
знаходимо



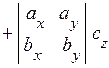
 .
.
Отже,

 . (1.25)
. (1.25)
Таким чином, змішаний добуток трьох векторів рівний визначнику третього порядку, який складається з відповідних координат векторів, що перемножуються.
Властивості змішаного добуток і його геометричне значення
1. Якщо в змішаному добутку поміняти місцями які-небудь два множники, то змішаний добуток змінить знак, наприклад:
 .
.
Дійсно, якщо в змішаному добутку поміняти місцями два множники, то це рівносильне тому, що у визначнику (1.25) поміняти місцями два ряди, а від цього визначник змінює знак на протилежний.
2. При циклічній перестановці множників змішаний добуток не змінюється:

 .
.
Якщо множники міняються місцями двічі, то у визначнику (2.25) рядок міняється місцями двічі, а від цього визначник не змінюється.
3. В змішаному добутку знаки векторного і скалярного добутку можна міняти місцями:
 .
.
Це витікає з властивості 2 і комутативності скалярного добутку. У зв'язку з цим змішаний добуток  (векторно-скалярний добуток) і
(векторно-скалярний добуток) і  (скалярно-векторний добуток) скорочено позначають
(скалярно-векторний добуток) скорочено позначають  .
.
4. Модуль змішаного добутку  рівний об'єму паралелепіпеда, побудованого на векторах
рівний об'єму паралелепіпеда, побудованого на векторах 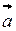 ,
, 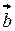 і
і  віднесених до загального початку:
віднесених до загального початку:
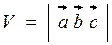 (1.26)
(1.26)
 Дійсно,
Дійсно,
|

Об'єм трикутної піраміди (тетраедра), побудованої на векторах 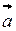 ,
, 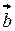 і
і  рівний шостій частині об'єму паралелепіпеда, тому
рівний шостій частині об'єму паралелепіпеда, тому
 . (1.27)
. (1.27)
5. Якщо змішаний добуток  додатній, то вектора
додатній, то вектора 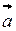 ,
, 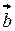 ,
,  утворюють праву трійку, а якщо від’ємний - то ліву.
утворюють праву трійку, а якщо від’ємний - то ліву.
6. Вектори 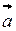 ,
, 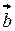 ,
,  компланарні тоді і тільки тоді, коли їх змішаний добуток рівний нулю.
компланарні тоді і тільки тоді, коли їх змішаний добуток рівний нулю.
Якщо  , то вектор
, то вектор  перпендикулярний до векторів
перпендикулярний до векторів  і лежить з векторами
і лежить з векторами 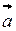 ,
, 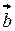 у одній площині. Це означає, що вектори
у одній площині. Це означає, що вектори 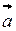 ,
, 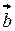 і
і  компланарні.
компланарні.
 Властивості 4 – 6 виражають геометричний зміст змішаного добутку трьох векторів.
Властивості 4 – 6 виражають геометричний зміст змішаного добутку трьох векторів.
Приклад 4.Обчислити об'єм тетраедра  з вершинами
з вершинами  ,
,  ,
,  ,
,  і його висоту
і його висоту  , опущену з вершини
, опущену з вершини  на грань
на грань 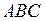 , якщо
, якщо  ;
;  ;
; 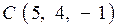 ;
;  .
.
Розв’язок.Об'єм тетраедра, побудованого на трьох не компланарних векторах рівний шостій частині абсолютної величини добутку векторів, витходячих з однієї вершини, що змішає, наприклад,  :
:
 .
.
Знайдемо вектори
 ;
;
 ;
;
 .
.
Об'єм тетраедра 

=  куб. од.
куб. од.
Площа грані 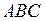 рівна половині площі паралелограма, побудованого на векторах
рівна половині площі паралелограма, побудованого на векторах  і
і  . Позначимо векторний добуток
. Позначимо векторний добуток  через
через 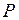 . Тоді модуль вектора
. Тоді модуль вектора 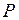 виражає собою площу паралелограма
виражає собою площу паралелограма


 .
.

 кв. од.
кв. од.
Об'єм тетраедра  , звідки знаходимо висоту
, звідки знаходимо висоту  :
:
 ед. довжини.
ед. довжини.
Відповідь.  куб. од.;
куб. од.;  од. довжини.
од. довжини.
Література
1. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. - К.: А.С.К., 2001. - 648 с.: іл. (Унів. б-ка). Бібліогр.: с. 632-633.
2. Вища математика. Збірник задач: Навч. Посібник / В.П.Дубовик, І.І.Юрик. І.П.Вовкодав та ін. За ред. В.П.Дубовика, І.І.Юрика. - К.: А.С.К., 2001. 480 с.: іл. (Унів. б-ка).
3. О.Н. Цубербиллер Задачи и упражнения по аналитической геометрии. Изд. 27-е. "Из-во Наука" М. 1966.
4. Крамарь Н.М., Швед О.П. Высшая математика. Курс лекций (часть I). -
Луганск: Из-во ВНУ им. В.Даля, 2002, - 200 с.
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |