Навигация:

Історія

Автоматизація

Адміністрування

Уточнення відокремленого кореня за методом простих ітерацій.

6.1. Представлення рівняння у нормальному вигляді. Представимо рівняння у нормальному вигляді тобто виберемо

6.2. Знаходження коефіцієнту стиску. Використовуючи додаток TrancsEq, одержуємо Так як , то ітераційний процес буде збіжним.

6.3. Побудова ітераційної схеми.

Старт. Як початкове (стартове) наближення можна вибрати будь-яке число. Виберемо число .

Ітераційний крок. Для заданого рівняння маємо

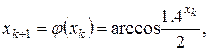
(1.5.28)

Момент зупинки. Зупинку ітераційного процесу для стискаючого відображення можна здійснювати як за числом ітерацій 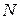, так і за величиною поточного кроку

6.4. Підрахунок числа ітерацій, яке забезпечить досягнення заданої точності.Для метода простих ітерацій для стискаючого відображення 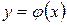з коефіцієнтом стиску вірна наступна оцінка похибки го наближення :

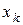. (1.5.29)

Тому для числа 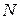– числа ітерацій, яке забезпечить досягнення заданої точності підрахунків, маємо формулу

, (1.5.30)

де - величина першого кроку і 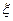- єдиний корінь (фікспункт) рівняння 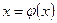, (тобто ).

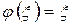Ця формула дає нам момент зупинки за числом ітерацій: для досягнення заданої точності 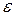потрібно виконати ітераційних кроків.

У нашому випадку

і 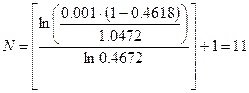. Обчислення зведемо у таблицю.

Таблиця 4.

Розрахункова таблиця знаходження кореня

рівняння за методом простих ітерацій

(зупинка за числом ітерацій)



1.04720	0.00000	1.04720
0.77958	1.04720	0.26761
0.86326	0.77958	0.08367
0.83858	0.86326	0.02468
0.84599	0.83858	0.00741
0.84377	0.84599	0.00221
0.84443	0.84377	0.00066
0.84424	0.84443	0.00020
0.844295	0.84424	0.000059
0.844278	0.844295	0.000018
0.844283	0.844278	0.000005

Зупинка обчислень – за числом ітерацій . Як наближене значення кореня беремо число з графи 11 рядка 1, тобто,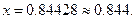

6.5. Підрахунок величини поточного кроку 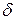, яке забезпечить досягнення заданої точності. Якщо в оцінці (1.5.28) вибрати за “нульовий крок” наближення і за наступне (“перше”) наближення 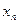, то одержуємо

(1.5.31)

Звідси, якщо виконана умова

, (1.5.32)

то і потрібна точність є досягнутою. У нашому випадку Обчислення зведемо у таблицю.

Таблиця 5.

Розрахункова таблиця знаходження кореня

рівняння за методом простих ітерацій

(зупинка за поточним кроком)

n

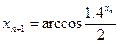
	1.04720	0.00000	1.04720
	0.77958	1.04720	0.26761
	0.86326	0.77958	0.08367
	0.83858	0.86326	0.02468
	0.84599	0.83858	0.00741
	0.84377	0.84599	0.00221
	0.84443	0.84377	0.00066

Зупинка за графою 4 (у рядку 7 маємо ). Як наближене значення кореня беремо число з графи 7 рядка 1, тобто, .

Висновки до лабораторної роботи.Отже, ми знайшли, що із заданою точністю рівняння має найменший за абсолютною величиною корінь х =-1.256 ± 0.001, а рівняння 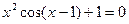має найменший за абсолютною величиною корінь х = 0.844 ± 0.001.

Варіанти індивідуальних завдань до роботи TransEq

Вар.

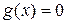
1.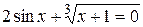

2.

3.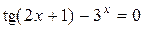

4.

5.

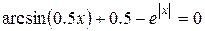
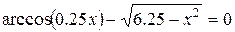
7.

8.

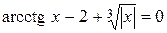
9.

10.

11.

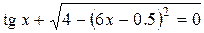
12.

13.

14.

15.

16.

17.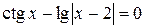

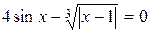
18.

19.

20.

21.

22.

23.

24.

25.

26.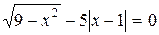

27.

28.

29.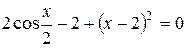

30.

31.

32.

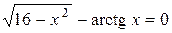
33.

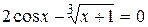
34.

35.

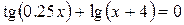
36.

37.

38.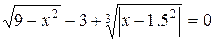

39.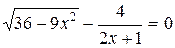

40.

41.

42.

43.

44.

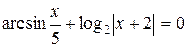
45.

46.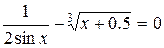

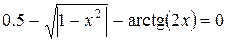
47.

48.

49.

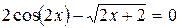
50.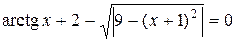

51.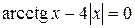

52.

53.

54.

55.

56.

57.

58.

59.

60.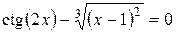

61.

62.

63.

64.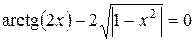

65.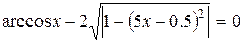

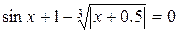
66.

67.

68.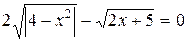

69.

70.

71.

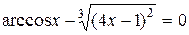
72.

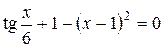
73.

74.

75.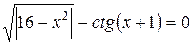

76.

77.

78.

79.

80.

81.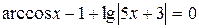

82.

83.

84.

85.

86.

87.

88.

89.

90.

91.

92.

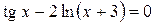
93.

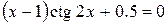
94.

95.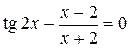

96.

97.

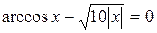
98.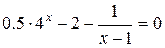

99.

100.

Додаткові матеріали до роботи TransEq

Інструкція користувачу для роботи з додатком TranscEq

Вхідний файл TranscEq.inp. Вхідний файл повинен бути у поточній теці (у якій розміщено додаток TranscEq). Структура вхідного файлу:

--------------------початок---------------------------

0,001 : e – точність знаходження кореня

- 1,3 : a – початок інтервалу

- 1,2 : b – кінець інтервалу

0,001 : h – крок (приріст аргументу х)

0 с – початок інтервалу для метода ітерацій

1 : d – кінець інтервалу для метода ітерацій

----------------------кінець ----------------------------

Робота з додатком TranscEq

1. Перед початком роботи потрібно підготувати записи функцій , , , 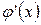як рядків програми на мові Object Pascal у вигляді result:=вираз;

2. Скопіювати повністю теку TranscEq (під тим же ім’ям) з сервера на власний магнітний носій (комп’ютер).

3. Завантажити Delphi 6 (Delphi 7), знайти і відкрити для змін файл проекту TranscEq.dpr.

4. Відкрити текстовий файл TranscEq.inp і встановити значення вхідних параметрів (кожен у окремому рядку з прогалиною після параметру, далі до кінця рядка – будь-яка послідовність символів)

e – точність знаходження кореня,

a,b – початок і кінець інтервалу, на якому відокремлено корінь ƒ(x)=0,

h – крок(приріст аргументу х), який використовуємо при знаходженні наближених значень

, , ,

, , .

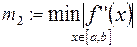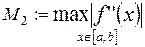c,d – початок і кінець інтервалу, на якому будемо шукати розв’язок рівняння (і на якому повинна виконуватись умова стискання ).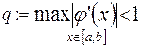

5. Відкрити модуль проекту TranscEq, змінити тіла функцій , , , 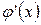на підготовлені раніше вирази. Скомпілювати змінений модуль.

6. Після завантаження змінений додаток TranscEq.inp створює форму (вікно додатку) з назвою Solving Transcendental Equations (Розв’язання трансцендентних рівнянь), відкриває файл TranscEq.inp і встановлює значення параметрів e,a,b,h,c,dу відповідних полях (типу TEdit) (ці значення можна далі змінювати перед натисканням інших кнопок на формі).

7. Введення параметрів e,a,b,h,c,dздійснюється натисканням кнопки Parameters Input(Введення параметрів). При цьому додатково шукаються наближено нулі функцій , , або констатується, що немає зміни знаків відповідних функцій (значення аргументу , що розглядаються, мають вигляд . Нормальною повинно бути поява у центрі форми трьох рядків Near root f: x=значення (Біля кореня f: x=значення), No roots f' (Нема коренів у похідної f'), No roots f’’ (Нема коренів у другої похідної f’’)” Якщо немає відокремлення кореня, тоді потрібно змінити інтервал і знову натиснути кнопку ParametersInput.

8. Для поліпшення пошуку нових значень 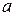, на формі присутня кнопка Max-Mins? (Максимуми – Мінімуми?), при натисканні якої на форму виводяться:

а) значення функцій , , на кінцях інтервалу ;

б) значення мінімумів і максимумів функцій , , та їх абсолютних значень , , на інтервалі . Пошук цих характеристик здійснюється на множині точок вигляду (якщо потрібно, можна зменшити відповідне значення h).

9. Розв’язання рівняння на інтервалі з відокремленим коренем за методом дихотомії здійснюється натисканням кнопки Dixotomy(Метод дихотомії). Знайдене значення кореня з’являється у середині форми. При цьому здійснюється виведення протоколу роботи додатку у текстовий файл Dixotomy.out, який можна переглянути будь-яким текстовим редактором (кодування Windows). Якщо немає відокремлення кореня або є похибки при заданні параметрів, здійснюється виведення вікна діагностики похибки Dihotomy method conditions is not satisfied(Умови для використання метода дихотомії не виконані).

10. Розв’язання рівняння на інтервалі з відокремленим коренем за методом хорд здійснюється натисканням кнопки Chords (Метод хорд). Знайдене значення кореня з’являється у середині форми. При цьому здійснюється виведення протоколу роботи додатку у текстовий файл Chords.out, який можна переглянути будь-яким текстовим редактором кодування (кодування Windows). Якщо немає відокремлення кореня або є похибки при заданні параметрів, здійснюється виведення вікна діагностики похибки Chords method conditions is not satisfied(Умови для використання метода хорд не виконані).

11. Розв’язання рівняння на інтервалі з відокремленим коренем за методом дотичних здійснюється натисканням кнопки Tangens (Метод дотичних). Знайдене значення кореня з’являється у середині форми. При цьому здійснюється виведення протоколу роботи додатку у текстовий файл Tangens.out, який можна переглянути будь-яким текстовим редактором кодування (кодування Windows). Якщо немає відокремлення кореня або є похибки при заданні параметрів, здійснюється виведення вікна діагностики похибки Tangens method conditions is not satisfied(Умови для використання метода хорд не виконані).

12. Розв’язання рівняння 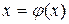на інтервалі за методом простих ітерацій з зупинкою за числом ітерацій (при умові наявності стискання) здійснюється натисканням кнопки Iterations-N (Метод простих ітерацій з зупинкою за N ітерацій). При цьому здійснюється виведення протоколу роботи додатку у текстовий файл Iter_N.out, який можна переглянути будь-яким текстовим редактором кодування (кодування Windows). Якщо немає відокремлення кореня або є похибки при заданні параметрів, здійснюється виведення вікна діагностики похибки Iterations method conditions is not satisfied(Умови для використання метода хорд не виконані).

13. Розв’язання рівняння 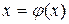на інтервалі за методом простих ітерацій з зупинкою за числом ітерацій (при умові наявності стискання) здійснюється натисканням кнопки Iterations-Step (Метод простих ітерацій з зупинкою за числом ітерацій). При цьому здійснюється виведення протоколу роботи додатку у текстовий файл IterStep.out, який можна переглянути будь-яким текстовим редактором (кодування Windows). Якщо на інтервалі 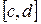нема стискання або є похибки при заданні параметрів, здійснюється виведення вікна діагностики похибки Iterations method conditions is not satisfied(Умови для використання метода простих ітерацій не виконані).

14. Завершення роботи з додатком TransEqздійснюється натисканням кнопки Закрити, що розташована у правому верхньому куті форми додатку.

7. Лабораторна робота NonLinSys на тему „Розв’язання систем нелінійних рівнянь”

Завдання.Графічно відокремити розв’язки системи двох нелінійних рівнянь з двома невідомими і наближено знайти ці розв’язки з точністю ε = 0.001 за методом Ньютона.

Хід виконання.Для заданої системи здійснити наступні дії:

А) Відокремити графічно розв’язки цієї системи, знаходячи точки перетину відношень і на площині, кожне з яких локально можна записати як деякі функції від і від . Знайти початкові (стартові) наближення { , }.

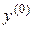Б) Уточнити один відокремлений розв’язок за методом Ньютона. Для цього:

1) Знайти якобіан .

2) Скласти ітераційну схему двовимірного метода Ньютона, тобто

а) Вибрати стартове наближення { , };

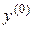б) Записати ітераційний крок: по-перше, розв’язати систему лінійних рівнянь (наприклад, за методом Гауса) відносно невідомих . Ця система лінійних рівнянь має матричний вигляд:

,

де 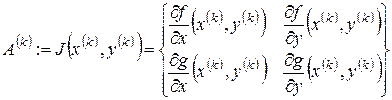- головна матриця системи, і, по-друге, знайти нове наближення за формулами .

в) Вибрати момент зупинки (за числом ітерацій N або за величиною поточного кроку , де 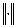- вибрана раніше векторна норма).

3) Провести обчислення трьох ітерацій без використання програми на ЕОМ. Обчислення звести в таблицю Таблиця 1(з наступними графами: Графа 1 – Номера ітерацій k; Графи 2,3 – наближення розв’язку на попередній ітерації; Графи 4,5 – прирости на поточному кроці; Графи 6,7 – нове наближення розв’язку , що одержано на k-й ітерації).

4) Написати на мові програмування Turbo Pascal власну програму Newton2d знаходження розв’язків системи нелінійних рівнянь за методом Ньютона або скористатись тією, що наведена у допоміжних матеріалах до лабораторної роботи. При цьому праві частини , , , , , 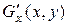потрібно реалізувати у окремому модулі (як тексти відповідних функцій) і процес ітерацій виводити в окремий текстовий файл.

5) Провести уточнення розв’язку, що відокремлений, за допомогою програми Newton2dдля ітерацій.. Порівняти результати таблиці 1 з підрахунками на ЕОМ.

6) Оформити звіт і захистити лабораторну роботу.

Теоретичні питання

1. Простір Rⁿ. Норма в Rⁿ. Приклад норм (m-норма, l-норма, k-норма).

2. Перетворення або 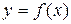. Якобіан перетворення .

3. Система нелінійних рівнянь 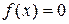у -вимірному просторі. Багатовимірний ітераційний метод Ньютона.

4. Умови збіжності метода Ньютона.

5. Системи лінійних рівнянь нормального вигляду 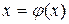у -вимірному просторі, де . Нерухомі точки (фікспункти) відображення .

6. Нерівність Ліпшиця для відображення . Стискуючі перетворення. Коефіцієнт стиску.

7. Головна теорема про розв’язок системи лінійних рівнянь нормального виду , де - стискуюче відображення.

8. Метод простих ітерацій у -вимірному просторі. Відповідна ітераційна схема.

Приклад виконання роботи NonLinSys

Предыдущая 1 2 3 4 5 6 7 8910 11 Следующая