Нередко помимо решения системы линейных уравнений по условию предварительно требуется исследовать её на совместность, то есть доказать, что какое-либо решение вообще существует. Ключевую роль в такой проверке играет теорема Кронекера-Капелли, которую я сформулирую в необходимом виде:

Если ранг матрицы системы равен рангу расширенной матрицы системы, то система совместна, причём, если данное число совпадает с количеством неизвестных, то решение единственно.

Таким образом, для исследования системы на совместность нужно проверить равенство 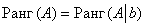, где – матрица системы (вспоминаем терминологию из урокаМетод Гаусса), а – расширенная матрица системы (т.е. матрица с коэффициентами при переменных + столбец свободных членов).

Всё просто:

Пример 7

Исследовать систему на совместность и найти её решение, если система совместна

А когда системы уже прорешаны – просто вдвойне… нет – втройне =)

Решение: тем не менее, обратим внимание на строгую верхнюю строчку – по условию,
в первую очередь, требуется проверить систему на совместность. Как начать решение?
В любом случае записываем расширенную матрицу системы и с помощью элементарных преобразований приводим её к ступенчатому виду:

а) Пример №1 статьи о методе исключения неизвестных:

Элементарные преобразования не меняют ранга матриц, поэтому в результате выполненных действий получены эквивалентные исходным матрица системы и расширенная матрица системы .

Максимальный порядок ненулевого минора матрицы системы равен трём. Здесь таковой минор в единственном экземпляре и совпадает он, понятно, с определителем самой матрицы:
(см. урок ометодах вычисления определителя)

Следовательно, .

Максимальный порядок ненулевого минора расширенной матрицы системы также равен трём:
(взяты первые два столбца + столбец свободных членов).

Таким образом, .

Вывод: , значит, по теореме Кронекера-Капелли система совместна; и поскольку количество переменных ( – 3 шт.) совпадает с рангом, то система имеет единственное решение.

Что дальше? Дальше следует непосредственно решить систему. Если по условию не предложен способ, то, конечно же, раскручиваем обратный ход метода Гаусса. Если требуется решить систему методом Крамера или с помощью обратной матрицы, ну что поделать….

б) Пример №1 статьи о несовместных системах и системах с общим решением:

В результате элементарных преобразований получена эквивалентная матрица системы и расширенная матрица системы .

Максимальный порядок ненулевого минора матрицы системы равен двум, например:
, поэтому

Заметьте, что здесь есть возможность выбрать и другой минор 2-го порядка, но проще всего в качестве примера взять ступенчатый определитель.

Максимальный порядок ненулевого минора расширенной матрицы системы равен трём, например:
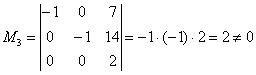(первые два столбца + столбец свободных членов).

Таким образом, .

Вывод: 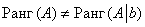, значит, по теореме Кронекера-Капелли система несовместна.

Однако помните – если по условию не требуется исследовать систему на совместность, то вполне достаточно ограничиться стандартным ответом (см. решение вышеуказанного урока).

в) Пример №3 той же статьи:

Максимальный порядок ненулевого минора матрицы системы равен двум, например:
, следовательно, .

Максимальный порядок ненулевого минора расширенной матрицы системы также равен двум, например:
, поэтому

Второй абзац можно полностью заменить хитрой лаконичной фразой: «по этой же причине ».

Вывод: , значит, по теореме Кронекера-Капелли система совместна. Поскольку ранг меньше количества переменных ( – 4 шт.), то система имеет бесконечно много решений.

Далее находим общее решение по стандартной схеме.

Готово.

Образец исследования системы на совместность также можно посмотреть в начале
Примера №1 урока о нахождении различных базисных решений системы.

…Всё-таки иногда удивительно обманываются ожидания – порой думаешь, что статья получится огромной, а она оказывается весьма компактной, а иногда, как сейчас – наоборот. Посмотрел статистику и жутко удивился добрым 20-ти тысячам символов. Поэтому всем высокого ранга и до скорых встреч!

Решения и ответы:

Пример 2:Решение: поскольку в матрице есть ненулевые элементы, то её ранг не меньше единицы.
, значит, ранг матрицы не менее двух.
Рассмотрим миноры 3-го порядка, при этом в них обязательно должен содержаться ненулевой минор . Таких миноров два:

Максимальный порядок ненулевого минора равен двум.
Ответ:

Пример 4:Решение: с помощью элементарных преобразований приведем матрицу к ступенчатому виду:

Совет 1: Как решать матрицу методом гаусса

Решение матрицы в классическом варианте находится с помощью метода Гаусса. Данный метод основан на последовательном исключении неизвестных переменных. Решение выполняется для расширенной матрицы, то есть с включенным столбцом свободных членов. При этом коэффициенты, составляющие матрицу, в результате проведенных преобразований образуют ступенчатую или треугольную матрицу. Относительно главной диагонали все коэффициенты матрицы, кроме свободных членов, должны быть приведены к нулю.

Статьи по теме:

Как решать матрицу методом гаусса
Как решить системы методом гаусса
Как решать уравнения методом Гаусса
Как решать матрицу по Гауссу
Что такое метод Джордана Гаусса

Вопрос «Как определить объем трубы?Если ее длина 200м а диаметр 65мм.» - 2 ответа

Инструкция

Определите совместность системы уравнений. Для этого посчитайте ранг основной матрицы А, то есть без столбца свободных членов. Затем добавьте столбец свободных членов и вычислите ранг получившейся расширенной матрицы В. Ранг должен быть отличным от нуля, тогда система имеет решение. При равных значениях рангов существует единственное решение данной матрицы.

Приведите расширенную матрицу к виду, когда по главной диагонали располагаются единицы, а ниже нее все элементы матрицы равны нулю. Для этого первую строку матрицы разделите на ее первый элемент так, чтобы первый элемент главной диагонали стал равен единице.

Отнимите первую строку от всех нижних строк так, чтобы в перовом столбце все нижние элементы обратились в ноль. Для этого помножьте сначала первую строку на первый элемент второй строки и отнимите строки. Затем аналогично помножьте первую строку на первый элемент третьей строки и отнимите строки. И так продолжайте со всеми строками матрицы.

Разделите вторую строку на коэффициент во втором столбце так, чтобы следующий элемент главной диагонали на второй строке и во втором столбце стал равен единице.

Отнимите вторую строку от всех нижних строк таким же образом, как описано выше. Все нижестоящие относительно второй строки элементы должны обратиться в ноль.

Аналогично проведите образование следующей единички на главной диагонали в третьей и последующих строках и обнуление нижестоящих коэффициентов матрицы.

Затем приведите полученную треугольную матрицу к виду, когда элементы над главной диагональю также представляют собой нули. Для этого отнимите последнюю строку матрицы из всех вышестоящих строк. Домножайте на соответствующий коэффициент и вычитайте стоки так, чтобы обратились в ноль элементы столбца, где в текущей строке имеется единичка.

Проведите подобное вычитание всех строк в порядке снизу вверх, пока не обнулятся все элементы выше главной диагонали.

Оставшиеся элементы в столбце свободных членов и являются решением заданной матрицы. Запишите полученные значения.

Немецкий бинарный опцион подарил мне роскошную жизнь

Я стала БОГАТОЙ в 19 лет с ЭТОЙ системой

tvoy-million.co

Немецкий Бинарный робот позволит зарабатывать по 500$ в ...

Совет 2: Как решать матрицу по Гауссу

Метод Гаусса является одним из основных принципов решения системы линейных уравнений. Его преимущество заключается в том, что оно не требует квадратичности исходной матрицы или же предварительного расчете ее определителя.

Вам понадобится

· Учебник по высшей математике.

Инструкция

Итак у вас есть система линейных алгебраических уравнений. Данный метод состоит из двух основных ходов - прямого и обратного.

Прямой ход:Запишите систему в матричном виде.Составьте расширенную матрицу и приведите ее к ступенчатому виду с помощью элементарных преобразований строк. Стоит напомнить, что матрица имеет ступенчатый вид, если выполняются следующие два условия: Если какая-то строка матрицы нулевая, то все последующие строки тоже являются нулевыми; Опорный элемент каждой последующий строки находится правее, чем в предыдущей.Элементарным преобразованием строк называют действия следующих трех типов:
1) перестановка местами любых двух строк матрицы.
2) замена любой строки суммой этой строки с любой другой, предварительно умноженной на некоторое число.
3) умножение любой строки на отличное от нуля число.Определите ранг расширенной матрицы и сделайте вывод о совместности системы. Если ранг матрица А не совпадает с рангом расширенной матрицы, то система не совместна и соответственно не имеет решения. Если же ранги не совпадают, то система совместна, и продолжайте поиск решений.

Обратный ход:Объявите базисными неизвестными те, номера которых совпадут с номерами базисных столбцов матрицы А (ее ступенчатого вида), а остальные переменные будете считать свободными. Число свободных неизвестных вычисляем по формуле k=n-r(A), где n-число неизвестных, r(A)-ранг матрица А.Далее вернитесь к ступенчатой матрице. Приведите ее к виду Гаусса. Напомним, что ступенчатая матрица имеет вид Гаусса, если все опорные элементы ее равны единице, а над опорными элементами одни нули. Запишите систему алгебраических уравнений, которая соответствует матрице вида Гаусса, обозначив свободные неизвестные как C1,...,Ck.На следующем шаге выразите из полученной системы базисные неизвестные через свободные.

Подробнее: http://www.kakprosto.ru/kak-27556-kak-reshat-matricu-metodom-gaussa#ixzz44rsCmPex

Загрузка...

1 2 3 4 56