Деякі відомості з векторного аналізу

Ґрадієнт.Розглянемо скалярне поле, тобто область простору, кожній точці якої відповідає визначене значення скаляра φ:

φ=φ(P)=φ(r)=φ(x₁,x₂,x₃),

де r - радіус-вектор, x₁,x₂,x₃ - декартові координати точкиP

Усім точкам поверхні, обумовленої рівнянням

φ(х₁, х₂,x₃) = const, ( 1)

відповідає однакове значення φ_. Поверхня виду ( 1) називається

поверхнею рівня скаляра φ. Поверхню рівня можна провести через будь-яку точку поля.

При зсуві з точки Р на відрізок dr функція φ отримує приріст

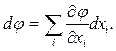
Останній вираз не залежить від вибору координат х_і ,тобто представляє собою інваріант. Сукупність величин dx_i утворює вектор dr.

Отже можна стверджувати, що величини dφ/dx_і, суть проекції деякого вектора на осі х_і. Цей вектор називають градієнтом скаляра φ і позначають символом grad φ. Отже,

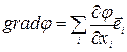(2)

або

Визначення (2) легко поширити на простір п вимірів. В останньому випадку число доданків у формулі (2) буде дорівнює не трьом, а п.

Доведемо, що компоненти градієнта перетворяться по формулах як компоненти вектора. Узявши дві системи координат: К і К', можна написати

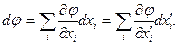
Виразимо dx_і через dx'_k і підставимо ці значення в (3):

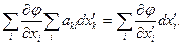
Змінимо в лівій частині порядок сумування по індексах i і k:

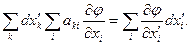
Індекси і та к є «німими». Як уже відзначалося, «німий» індекс можна позначати будь-якою буквою. Тому сума ліворуч не зміниться, якщо переставити індекси i і k. У підсумку одержимо

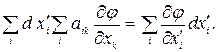
З отриманого нами співвідношення випливає

Таким чином, ми показали, що величини дφ/дх_і при перетвореннях координат поводяться як компоненти вектора.

Гамільтон увів векторний диференціальний оператор Ñ (оператор набла чи оператор Гамільтона), що являє собою вектор зі складовими д/дх, д/ду, д/дz:

(4)

Сам по собі вектор Ñ змісту не має. Він набуває сенсу, будучи застосований до скалярної чи векторної функції. Так, при символічному множенні Ñ на φ виходить градієнт φ:

Отже, Ñφ = grad φ. Згідно (3) приріст φ може бути представлений у вигляді скалярного добутку векторів grad φ і dr:

dφ = grad φ • dr = (Ñφ) dr. (5)

При переміщенні по поверхні рівня φ залишається незмінною (dφ = 0). Звідси відповідно до (5) випливає, що вектор Ñφ у кожній точці поля спрямований по нормалі до поверхні рівня. Знайдемо швидкість зміни φ уздовж деякого напрямку l, тобто dφ/dl. Згідно (5) приростом φ на відрізку dl дорівнює (Ñφ) dl = (Ñφ)_l dl, де (Ñφ)_l—проекція градієнта на напрямок l.

Тому

.

Таким чином, проекція градієнта на деякий напрямок дає швидкість зміни функції в даному напрямку.

Відзначимо, що вектор Ñφ існує в кожній точці скалярного поля φ. Отже, градієнт утворює векторне поле, тобто область простору, кожній точці якої відповідає визначене значення вектора Ñφ.

Дивергенція.

Нехай нам дане поле вектора а. Потоком вектора а через поверхню fназивається вираз

, (6)

де а_n — проекція вектора а на позитивну нормаль до площадки df, df— вектор елементарної площадки, його модуль дорівнює величині площадки df, а напрям збігається з напрямом позитивної нормалі до площадки. Напрямок позитивної нормалі визначається в залежності від обставин. Так, наприклад, при обчисленні потоку через замкнуту поверхню позитивною вважається зовнішня нормаль. Назва «потік» обумовлене тим, що у випадку поля вектора швидкості рідини інтеграл ( 6) дає потік рідини через поверхню f , тобто об’єм рідини, що протікає через fза одиницю часу. Оточимо точку Р поля замкнутою поверхнею f. Обчислимо потік Ф_a через цю поверхню. Відношення Ф_а до V буде характеризувати властивості поля біля точки Р, усереднені по об’ємі V, усередині f. Чим менше лінійні розміри об’єму, тим ближче буде середня характеристика до даної характеристики поля в точці Р. Скалярну величину

(7)

називають дивергенцією векторного поля в точці Р.

мал.1

Визначення (7) є самим загальним, що не залежить від вибору координатної системи. Знайдемо вираз для дивергенції через проекції а на осі декартової системи координат. Візьмемо в околі точки Р об’єм у вигляді прямокутного паралелепіпеда з гранями,

перпендикулярними до координатних осей (мал. 1). Знайдемо потік вектора а через грані 1 і 2, які перпендикулярні до осі х. Зовнішня нормаль до грані 1 збігається по напрямку з віссю х. Тому для цієї грані а_п = a_xl (індекс 1 указує, що значення а_х береться в точці, що лежить на грані 1). Зовнішня нормаль до грані 2 протилежна по напрямку осі х. Тому для неї а_п = - a_x2 (індекс 2 вказує, що значення а_х береться в точці, що лежить на грані 2). Сумарний потік через грані 1 і 2 дорівнює

(8)

де df = df₁ = df₂ (див. мал. l), a_x1 і a_x2 беруться для точок граней 1 і 2 з однаковими у і z. Інтеграл, що стоїть праворуч, береться по поверхні f кожної з граней 1 і 2. Розкладемо а_х у ряд в околі точки Р:

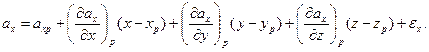(9)

Тут х_р, у_р, z_p — координати точки Р, а_хР — значення а_х у точці Р, (да_х/дх)_Р і т. д. - значення похідних у точці Р, ε_х — величина більш високого порядку малості, чим різниці (х— х_р), (у — у_р), (z— z_p), тобто величина, що зменшується швидше, ніж лінійні розміри паралелепіпеда.

Поклавши у рівняння (9) x = x₁, знайдемо значення а_х у точках грані 1 тобто а_х1; поклавши x=x₂, одержимо значення a_x2. Віднявши ці значення один із одного, одержимо для протилежних площадок df_l і df₂ (значення y i z для них однакові):

де знов-таки ε'_х - величина, що зменшується швидше, ніж лінійні розміри об’єму.

Підставивши знайдене нами значення у формулу (8), одержимо

З мал. 1 видно, що добуток (х₁- х₂)f дає об’єм паралелепіпеда V. Тому:

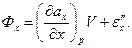
де ε"_х — величина більш високого порядку , ніж V.

Аналогічні вирази виходять і для потоків через пари граней, перпендикулярних до осей у і z:

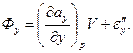
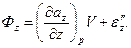
Склавши разом Ф_х, Ф_у і Ф_r, одержимо повний потік вектора а через поверхню паралелепіпеда. Розділивши відповідно до рівняння (7) цей потік на V і зробивши граничний перехід) V →Р, прийдемо до формули

(10)

(через непотрібність ми опустили індекс Р при похідних). Знайдений нами вираз ( 10) для дивергенції можна записати у вигляді

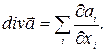(11)

У такій формі поняття дивергенції може бути поширене на векторні поля в просторі n вимірів. Визначення (7) також можна поширити на простір n вимірів. У цьому випадку під елементом об’єму варто розуміти dV*=dx₁ dx₂ dx₃. .dx_n

Інтеграл потрібно брати по гіперповерхні розмірності п —1. Елемент гіперповерхні, перпендикулярний до осі x_k буде дорівнювати df*= dx₁ dx₂... dx_k-_l dx_k+l. . .dx_n.

У просторі чотирьох вимірів гіперповерхнею буде звичайний тривимірний об’єм. Рівняння (11) можна розглядати як суму добутків величин Ñ_і = д/дх_і і a_і тобто як скалярний добуток векторів Ñ і а. Тому дивергенцію можна представити у вигляді

diva=Ña. (12)

Величина (Ñа)існує в кожній точці векторного поля а.

Отже, дивергенція утворить скалярне поле, визначене в тій же частині простору, що і поле вектора а. Візьмемо в поле вектора а кінцевий об’єм V, обмежений поверхнею f (2). Розіб'ємо цей об’єм на елементарні об’єми DV. Згідно (7) для потоку DФ_а через поверхню такого об’єму можна написати DФ_а = diva×DV = Ña×DV. Складемо ці рівняння для всіх елементарних об’ємів. мал. 2.

При сумуванні DФ_а потоки через грані, що розділяють два сусідніх об’єми, взаємно знищаться (для суміжних об’ємів потоки відрізняються знаками, тому що зовнішні нормалі n і n' мають протилежні напрямки). Некомпенсованими залишаться тільки потоки через ділянки зовнішньої поверхні f, так що в сумі вийде потік вектора а через цю поверхню. Сума праворуч у границі (при DV—»0) перетвориться в інтеграл по всьому об’ємі. Наближена рівність у границі перейде в строгу рівність. У результаті одержимо

(13)

Отримане нами співвідношення називається теоремою Остроградського — Гауса. Словесне формулювання цієї теореми говорить: потік вектора через замкнуту поверхню дорівнює інтегралу від дивергенції по об’ємі, обмеженому цією поверхнею.

Ротор.

Циркуляцією вектора а по контурі Г називається вираз

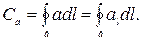(14)

Наприклад, у потенціальному полі сила циркуляції вектора F дорівнює роботі сил на замкнутому контуру Г.

Візьмемо в околі точки Р контур Г, що лежить у площині, що проходить через Р. Знайдемо циркуляцію С_а по цьому контурі. Відношення С_а до поверхні f, охоплюваної контуром, буде характеризувати властивості поля в околі точки Р, усереднені по поверхні l. Чим менше лінійні розміри поверхні, тим ближче буде середня характеристика до дійсної характеристики поля в точці Р. У границі, при стягуванні контуру до точки Р, середня характеристика перетвориться в дійсну. Таким чином, властивості векторного поля в деякій точці Р можна охарактеризувати величиною

(15)

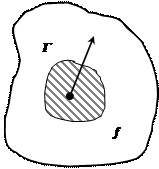Величина (15) залежить не тільки від властивостей поля в точці Р, але і від орієнтації площини, у якій лежить контур. Орієнтацію цієї площини в просторі можна задати нормаллю до площини, зв'язаної з напрямком обходу по контурі Г при інтегруванні правилом правого гвинта (мал. 3). Для різних напрямків n величина ( 15) буде мати в одній і тій же точці Р різне значення, причому, як легко зміркувати, протилежним напрямкам n відповідають значення величини ( 15), що відрізняються тільки знаком. Отже, величина, обумовлена формулою (15), поводиться як проекція деякого вектора на напрямок нормалі до контуру Г. Цей вектор називають ротором векторного поля в точці Р и позначають символом rot a. Таким чином,

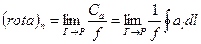. (16)

мал..4

Формула ( 16) дає саме загальне визначення ротора, що не залежить від вибору координатної системи. Знайдемо вираження для ротора через проекції вектора rot×a на вісь х. Для цього візьмемо в околі точки Р контур Г, що лежить у площині, перпендикулярної до осі х (мал. 4). Напрямок обходу по контурі виберемо так, щоб воно утворювало з напрямком осі х. правогвинтову систему. Тоді напрямок n і осі х збіжаться і вираз (16) дасть (rot×a)_x. Для вибраного нами контуру

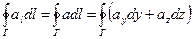
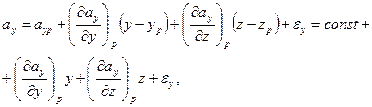
де const включає в себе три складових, які не залежать від y і z, e_у-величина більш високого порядку малості, чим лінійні розміри контуру. Отже,

Легко зміркувати, що ∮dy = 0. Точно так само дорівнює нулю інтеграл

.

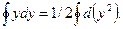З мал. 4 неважко побачити, що ∮zdy = -f де f- площа контуру. Отже

(17)

де e_у' -величина більш високого порядку малості, чим площа контуру f.

Зробивши аналогічні перетворення для a_z, отримаємо вираз

Інтеграли ∮dz і ∮zdz = 1/2∮d(z²) дорівнюють нулю, ∮ydz = f

Тому

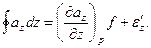
Вирази (17) і (18) у сумі дають ∮a_ldl. Розділивши відповідно до виразу (16) цю суму на f і здійснивши граничний перехід, одержимо

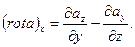
Розглянувши циркуляцію для контурів, орієнтованих нормаллю n по осях у і z, можна одержати вираження для проекцій ротора на ці осі:

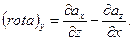
Формули для проекцій ротора на координатні осі легко запам'ятати, прийнявши до уваги, що в кожній з них індекс при rot∙a і букви, що стоять праворуч у знаменниках, утворять циклічну перестановку, здійснювану за схемою: х→у→z→x. Знаючи проекції, легко знайти сам вектор:

(19)

З врахуванням того, що, наприклад, да_г/ду можна представити у вигляді Ñ_уа_г і т.д. , запишемо формулу (19) у такий спосіб:

(20)

Нарешті, порівняння з формулою (VI. 31) дає нам право написати, що

rot∙a = [Ña] (21)

Скориставшись формулами для векторного добутку, можна написати для ротора і його k-й компоненти наступні вирази:

Величина [Ña] існує в кожній точці векторного поля а. Отже, ротор утворить векторне поле, визначене в тій же частині простору, у якій задане поле вектора а. Візьмемо в поле вектора а довільну поверхню f, обмежену контуром Г (контур може бути будь-яким, не обов'язково плоским). Розіб'ємо цю поверхню на малі елементи ∆f (мал. 5). Згідно (16) для циркуляції ∆С_а по границі елемента ∆f можна написати вираз ∆С_а =[Ña]_n ∆f, де [Ña]_n — проекція [Ña] на нормаль до даного ∆f, зв'язану з напрямком обходу правилом правого гвинта.

Складемо ці формули для всіх ∆f. При сумуванні ∆С_а інтеграли ∫a_l dl, узяті вздовж границі сусідніх площадок, взаємно знищаться (для суміжних площадок ці інтеграли відрізняються знаком, тому що беруться в різних напрямках). Некомпенсованими залишаться тільки інтеграли ∫a_ldl для ділянок, що збігаються з контуром Г, що обмежує f. Ці інтеграли дадуть у сукупності циркуляцію а по контурі Г. Сума праворуч у границі (при ∆f→0) перетвориться в інтеграл по поверхні. Наближена рівність у межі перейде в строгу рівність. У підсумку одержимо

(23)

Знайдене нами співвідношення називається теоремою Стокса. Словесне формулювання цієї теореми говорить: циркуляція вектора а по замкнутому контурі Г дорівнює потоку вектора [Ña] через поверхню, натягнуту на контур Г.

Поверхня, по якій береться інтеграл у правій частині формули (23), може бути будь-якою, важливо лише, щоб вона спиралася своєю границею на контур Г. Напрямок нормалі n повинен бути погоджений з напрямком обходу контуру Г при інтегруванні.

Застосування оператора Ñ до добутку функцій.

При складанні формул, до яких входить Ñ, потрібно керуватися як правилами векторної алгебри, так і правилами диференціального числення. Нехай, наприклад, φ і y— скалярні функції точки. Тоді

Ñ(φy)=Ñ_y(φy)+Ñ_φ(φy) ( 24)

(індекс при Ñ вказує, на яку з функцій вона діє). Співмножник, на який у даний момент посилається Ñ не діє, можна винести з-під знаку Ñ (оператор Ñ діє тільки на величини, що стоять за ним). Тоді формула (24) прийме вигляд Ñ(φy) = φÑ_yy + yÑ_φ φ. У написаному нами вираженні, мабуть, немає необхідності в індексах при Ñ, так що остаточно

Ñ(φy) = φÑy + yÑφ. (25)

(читається: «фі градієнт псі плюс псі градієнт фі»).

Застосуємо Ñ до добутку φ∙а. У цьому випадку мається дві можливості — вектори Ñ і φа можна перемножити як скалярно, так і векторно. Відповідно одержимо

Ñ(φa) = Ñ_φ(φa) + Ñ_a(φa)=aÑφ + φÑa (26)

(«а градієнт фі плюс фі дивергенція а»),

[Ñ,(φа)=[Ñ_φ,(φа)]+[Ñ_а,(φа)]=[(Ñφ),а] + φ[Ña]. (27)

Тепер застосуємо Ñ до добутку [ab], перемноживши вектори спочатку скалярно: Ñ[ab]=Ñ_а[ab] –Ñ_в[ab]. Здійснимо в кожному з доданків циклічну перестановку Ñ[a,b]=b[Ñ_aa]+a[bÑ_b]=b[Ñ_aa]-a[Ñ_bb]

Опустивши непотрібні вже індекси, прийдемо до формули

Ñ[ab]=b[Ña] — a[Ñb] ( 28)

(«b ротор а мінус а ротор b»).

Помножимо [ab] на Ñ векторно: [Ñ,[ab]] = [Ñ_а,[ab]] + [Ñ_b,[ab]]. Розгорнемо кожне з доданків по формулі «бац мінус цаб»):

[Ñ,[ab]] = a(Ñ_аb) — b(Ñ_aa) + a(Ñ_bb)— b(Ñ_ba).

Розставивши множники так, щоб можна було опустити індекси при Ñ, одержимо

[Ñ,[ab]] = (bÑ)a — (aÑ)b + a(Ñb)— b(Ña). ( 29)

Вирази (aÑ) і (bÑ) суть скалярні диференціальні оператори. Наприклад,

(30)

Ці оператори можуть застосовуватися як до скалярних, так і до векторних функцій. У застосуванні до скаляра φ оператор (30) дає

(31)

При дії оператора (aÑ) на вектор b отримуємо вираз

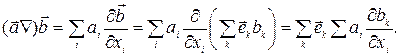(32)

Застосуємо оператора (30) до добутку скалярної функції φ і векторної функції b:

(33)

Корисно знати значення виразу (aÑ)r, де r - радіус-вектор, а-деякий довільний вектор. Підставивши в (32) r замість b і прийнявши до уваги, що ∂x_k/∂x_i = d_ik, одержимо

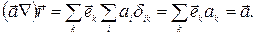(34)

Формули (25) — (29) ми одержали легко. Складніше знайти градієнт скалярного добутку двох векторів: Ñ (a b), тому що неясно, що треба розуміти під, наприклад, виразом Ñ_a(a b). Його не можна трактувати як (Ñ_a ∙a )b, тому що операції перемножування а з b і застосування Ñ_a не можна переставляти. Це можна обійти, скориставшись допоміжними співвідношеннями, що випливають з формули «бац мінус цаб»:

[а, [Ñb]] = Ñ_b(a∙ b)—b(Ñ_ba) = Ñ_b(a∙ b) —(aÑ)b,

звідси

Ñ_b(a∙ b) = [a,[Ñb]]+(aÑ)b. (35)

Записавши таким же способом [b, [Ña]], прийдемо до співвідношення

Ñ_а(a∙ b) = [b, [Ña]]+(bÑ)a. (36)

Підстановка співвідношень (35) і (36) у формулу

Ñ (a∙b)= Ñ_a(a b)+ Ñ_b(a b)

приводить до наступного виразу для градієнта скалярного добутку векторів а і b:

Ñ(a∙b)=[a,[Ñb]]+[b,[Ña]]+(a∙Ñ)b + (bÑ)a. (37)

Повторне застосування оператора Ñ.

У результаті впливу оператора Ñ на скалярні чи векторні функції отримуються нові векторні або скалярні функції, до яких у свою чергу можна бути застосований оператор Ñ.

Градієнт функції φ є вектор. Отже, до нього можуть бути застосовані операції і дивергенції, і ротора. Обчислимо дивергенцію градієнта. Відповідно до формул (2) і (11)

Таким чином,

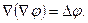(38)

де ∆-оператор Лапласа:

(39)

З пророблених нами операцій випливає, що

Ѳ = ∆. (40)

Однак потрібно мати на увазі, .що таке співвідношення між операторами Ñ і ∆ має місце тільки в декартових координатах. В інших системах координат, наприклад у циліндричній або сферичній, співвідношення (40) не виконується. Загальним визначенням оператора ∆, справедливим у будь-якій системі координат, є визначення, що випливає зі співвідношення (38), яке можна записати у вигляді

(41)

Знайдемо rot∙grad∙φ. Згідно (22)

(42)

Оскільки ∂²φ/∂х_і ∂х_к =∂²φ/∂х_к∂х_і, останній вираз дорівнює нулю, так що

rot∙grad∙φ = 0 (43)

Цього і треба було очікувати, тому що [Ñ, Ñφ] = [ÑÑ]φ, а векторний добуток вектора на самого себе дорівнює нулю.

Обчислимо дівергенцію ротора. Відповідно до формул (11) і (22)

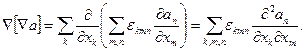
Тому що d²a_n/dx_kdx_m = d²a_n/dx_mdx_k, останній вираз дорівнює нулю. Отже,

div∙rota = 0. (44)

До цього результату можна було прийти відразу, прийнявши до уваги, що мішаний добуток векторів (яким є Ñ[Ña]) дорівнює об’єму паралелепіпеда, побудованого на векторах, що перемножуються. Тому при збігу двох співмножників із трьох такий добуток дорівнює нулю.

Для обчислення rot rot а будемо виходити з формул (22):

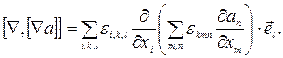
Зробимо циклічну перестановку індексів при ε так, щоб індекс k в обох ε виявився на останньому місці . У підсумку отримаємо

Здійснимо сумування по індексах m i n. У результаті отриманий нами вираз прийме вигляд

,

що можна представити в такий спосіб:

Отже ми отримали формулу

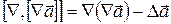(45)

або

(46)

Легко переконатися в тому, що співвідношення ( 45) можна одержати, якщо розгорнути [Ñ,[Ña]] по формулі «бац мінус цаб», працюючи при цьому з Ñ як зі звичайним вектором.

З (46) випливає, що

(47)

Дивергенція є скаляром. Тому ніякої операції, окрім операції знаходження градієнта, до неї застосувати не можна.