
Кафедра прикладної математики та математичного моделювання
|
|

МЕТОДИЧНІ РЕКОМЕНДАЦІЇ
До самостійного вивчення вищої математики
на економічному факультеті
Розділ ІІІ. Аналітична геометрія.
I курс, 1 семестр.
Кременчук
Розповсюдження і тиражування без офіційного дозволу ІЕНТ і авторів заборонено.
Методичні рекомендації до самостійного вивчення вищої математики на економічному факультеті
(розділ ІІІ. Аналітична геометрія. I курс, 1семестр).
Укладач: Тристан Віктор Миколайович, старший викладач.
Рецензент: Семенов В.О, кандидат фізико-математичних наук, професор.
Комп’ютерний набір: Тристан А.В.
Відповідальний за випуск: професор Семенов В.О.
Методичні рекомендації розглянуті та рекомендовані до видання на засіданні кафедри прикладної математики та математичного моделювання від 30 серпня 2003р., протокол № 1
Схвалено методичною радою ІЕНТ “_____”_______________р.,
протокол №______.
Затверджено Вченою радою ІЕНТ “_____”_______________р.,
протокол №______.
Наклад 21 примірників
Передмова
Методичні рекомендації адресовані студентам економічного факультету, які навчаються за спеціальностями „Облік та аудит” і „Маркетинг” стаціонарно та заочно. Вони містять необхідний теоретичний матеріал і розв’язання типових задач ІІІ розділу курсу вищої математики для економістів „Аналітична геометрія”, що вивчається в першому семестрі.
Мета методичних рекомендацій полягає у тому, щоб допомогти студентам засвоїти цей розділ курсу вищої математики та набути навичок самостійної роботи при розв’язуванні задач.
Методичні рекомендації містять завдання контрольної роботи в 34 варіантах.
З метою самоконтролю за вивченням курсу до методичних рекомендацій внесено питання для підготовки до екзамену.
Методичні рекомендації містять список рекомендованої літератури.
І. Основні питання, що вивчаються в розділі „Аналітична геометрія”.
- Рівняння ліній на площині.
- Пряма на площині.
2.1. Загальне рівняння . Нормальний вектор прямої;
2.2. Канонічне рівняння. напрямний вектор;
2.3. Рівняння прямої, що проходить через дві точки;
2.4. Рівняння прямої з кутовим коефіцієнтом;
2.5. Нормальне рівняння прямої. Нормувальний множ-
ник. Відстань від точки до прямої;
2.6. Кут між двома прямими на площині. Умови пара-
лельності та перпендикулярності прямих.
- Площина у просторі.
3.1. Загальне рівняння площини. Нормальний вектор;
3.2. Рівняння площини, що проходить через три задані
точки;
3.3. Нормальне рівняння площини. Нормувальний множник. Відстань від точки до площини;
3.4. Кут між двома площинами. Умови паралельності
та перпендикулярності двох прямих.
Пряма у просторі.
4.1. Канонічні рівняння прямої;
4.2. Параметричні рівняння прямої;
4.3. Загальні рівняння прямої;
4.4. Умови паралельності та перпендикулярності
прямих;
4.5. Умови паралельності та перпендикулярності
прямої та площини.
Криві другого порядку.
5.1. Коло. Еліпс;
5.2. Гіпербола;
5.3. Парабола;
ІІ. Основні теоретичні відомості. Приклади розв’язання задач.
1. Рівняння ліній на площині.
Означення 1. Рівнянням лінії  на площині називається рівняння зі змінними х і у, якому задовольняють координати будь-якої точки М цієї лінії і не задовольняють координати кожної точки, що не належить до
на площині називається рівняння зі змінними х і у, якому задовольняють координати будь-якої точки М цієї лінії і не задовольняють координати кожної точки, що не належить до  . При складанні рівнянь використовують векторну алгебру.
. При складанні рівнянь використовують векторну алгебру.
2. Пряма на площині.
Загальне рівняння прямої. Нормальний вектор.
Нехай на площині задано точку  та вектор
та вектор  . Складемо рівняння прямої, що проходить через точку
. Складемо рівняння прямої, що проходить через точку  перпендикулярно вектору
перпендикулярно вектору  . Візьмемо довільну точку прямої
. Візьмемо довільну точку прямої  , тоді вектор
, тоді вектор  перпендикулярний вектору
перпендикулярний вектору  , тому скалярний добуток
, тому скалярний добуток  , або
, або  . Звідки одержуємо загальне рівняння прямої
. Звідки одержуємо загальне рівняння прямої 
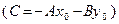 (2.1)
(2.1)
Означення 2. Загальним рівнянням прямої називають рівняння вигляду  . Вектор
. Вектор  - нормальний вектор прямої,заданої загальним рівнянням.
- нормальний вектор прямої,заданої загальним рівнянням.
Приклад 1
Побудувати лінію, рівняння якої 2х – у = 4 Записати нормальний вектор.
Розв’язання.
За означенням 2 дане рівняння – це загальне рівняння прямої. Знайдемо координати двох точок, що належать даній прямій: якщо х=0, то у=–4 , якщо у=0, то х=2. Отже, пряма проходить через точки 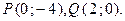

|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |