
Прості та складені випадкові події. Простір елементарних подій
|
|
Для математичного опису випадкових подій — наслідків експерименту — застосовують такі точні поняття: прості (елементарні) та складені випадкові події, простір елементарних подій.
Подія, що може відбутися внаслідок проведення однієї і лише однієї спроби (експерименту), називається простою (елементарною) випадковою подією. Елементарні події позначаються 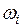 , (і=1, 2, 3,...) і в теорії ймовірностей, так само як, скажімо, точка в геометрії, не поділяються на простіші складові.
, (і=1, 2, 3,...) і в теорії ймовірностей, так само як, скажімо, точка в геометрії, не поділяються на простіші складові.
Приклад 1. Монету підкидають один раз. Визначити елементарні події цього експерименту.
Розв'язання. Можливі такі елементарні випадкові події:  =г (монета випаде гербом);
=г (монета випаде гербом); 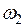 =ц (монета випаде цифрою).
=ц (монета випаде цифрою).
Приклад 2. Монету підкидають двічі. Визначити елементарні події цього експерименту.
Розв'язання. Дворазове підкидання монети — це одна спроба. Елементарними випадковими подіями будуть:  =гг (двічі випаде герб);
=гг (двічі випаде герб); 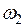 =цц (двічі випаде цифра);
=цц (двічі випаде цифра);  =гц і
=гц і  =цг.
=цг.
Отже, цьому експерименту відповідають чотири елементарні події.
Випадкова подія називається складеною, якщо її можна розкласти на прості (елементарні) події. Складені випадкові події позначаються латинськими великими літерами: A, B, C, D.
Приклад 3. Задано множину чисел 
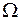 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Навмання із цієї множини беруть одне число. Побудувати такі випадкові події: 1) з'явиться число, кратне 2; 2) число кратне 3; 3) число, кратне 5. Ці випадкові події будуть складеними. Позначимо їх відповідно А, В, С. Тоді А = = {2, 4, 6, 8, 10, 12}; В = {3, 6, 9, 12}; С={5, 10,}.
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Навмання із цієї множини беруть одне число. Побудувати такі випадкові події: 1) з'явиться число, кратне 2; 2) число кратне 3; 3) число, кратне 5. Ці випадкові події будуть складеними. Позначимо їх відповідно А, В, С. Тоді А = = {2, 4, 6, 8, 10, 12}; В = {3, 6, 9, 12}; С={5, 10,}.
Елементарні випадкові події “5” та “10” називають елементарними подіями, які сприяють появі подій С унаслідок проведення експерименту.
Кожному експерименту (спробі) з випадковими результатами (наслідками) відповідає певна множина 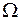 елементарних подій, кожна з яких може відбутися (настати) внаслідок його проведення. Множину
елементарних подій, кожна з яких може відбутися (настати) внаслідок його проведення. Множину 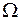 називають простором елементарних подій.
називають простором елементарних подій.
Простір елементарних подій може бути як дискретним, так і неперервним. Якщо множина є зчисленною (зліченною), тобто всі її елементи можна перелічити або принаймні пронумерувати (кожній елементарній події поставити у відповідність один і тільки один елемент нескінченної послідовності натуральних чисел 1,2,3, ...), то простір елементарних подій називають дискретним. Він може бути обмеженим і необмеженим.
У противному разі (тобто коли кожній елементарній події не можна поставити у взаємно однозначну відповідність певне натуральне число) простір елементарних подій називають неперервним.
У розглянутих раніше прикладах простори елементарних подій були дискретними.
Приклади неперервних (недискретних) просторів елементарних подій дістанемо, розглянувши: розміри однотипних деталей (діаметр, довжина), що їх виготовляє робітник або верстат-автомат; покази приладів, що вимірюють масу, силу струму, напругу, опір і т. ін.
Отже, поняття елементарної події, простору елементарних подій є основними в теорії ймовірностей, як точка та пряма в аксіоматично побудованій евклідовій геометрії. Сама природа елементарних подій у теорії ймовірностей при цьому неістотна.
Операції над подіями
Додавання. Сумою двох подій А і В називається така подія С=А 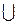 В (С=А + В), яка внаслідок експерименту настає з настанням хоча б однієї з подій А або В. Подію А
В (С=А + В), яка внаслідок експерименту настає з настанням хоча б однієї з подій А або В. Подію А 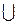 В схематично зображено на рис. 1 заштрихованою областю.
В схематично зображено на рис. 1 заштрихованою областю.

Рис. 1 Операція об 'єднання подій А і В.
Множення. Добутком двох подій А і В називається така подія С = А 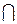 В (С = АВ), яка внаслідок експерименту настає з одночасним настанням подій А і В.
В (С = АВ), яка внаслідок експерименту настає з одночасним настанням подій А і В.
Операція А 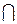 В називається перерізом цих подій (рис. 2).
В називається перерізом цих подій (рис. 2).

Рис. 2. Переріз подій А і В.
Приклад. Перерізом подій А = {2, 4, 6, 8, 10, 12} і В = {3, 6, 9, 12} є подія С1 = {6}, а сумою є подія С2 = {2, 3, 4, 6, 8, 9, 10, 12}.
Якщо 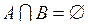 , то випадкові події А і В називають несумісними. Якщо
, то випадкові події А і В називають несумісними. Якщо 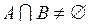 , то такі випадкові події А і В називають сумісними.
, то такі випадкові події А і В називають сумісними.
Повна група подій. Якщо  , то такі випадкові події утворюють повну групу, а саме: внаслідок експерименту якась із подій {Аi} обов'язково настане.
, то такі випадкові події утворюють повну групу, а саме: внаслідок експерименту якась із подій {Аi} обов'язково настане.
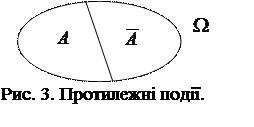
Протилежні події. Дві несумісні випадкові події, що утворюють повну групу, називають протилежними.
Подія, яка протилежна А, позначається 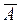 . Протилежні події у просторі елементарних подій ілюструє рис. 3.
. Протилежні події у просторі елементарних подій ілюструє рис. 3.
Елементарні випадкові події задовольняють такі твердження: 1) між собою несумісні; 2) утворюють повну групу; 3) є рівноможливими, а саме: усі елементарні події мають однакові можливості відбутися внаслідок проведення одного експерименту.
Питання для самоконтролю
1. Що називається вірогідною; неможливою подією? Навести приклади.
2. Яка подія називається випадковою? Навести приклади.
3. Яка подія називається елементарною; складеною випадковою подією? Навести приклади.
4. Що називається простором елементарних подій? Навести приклади.
5. Що називається сумою, добутком, різницею двох випадкових подій А і В?
Література
Обов’язкова: [1]. Додаткова:[1], [4], [7].
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |