Метод Ейлера для розв’язування задач Коші

Нехай потрібно розв’язати задачу (1-2) тоді при чисельному розв’язанні задачі (1) задача ставитиметься в наступному вигляді.

В точцах потрібно знайти наближення для точного значення , де - наближення, – точне

-крок сітки

.

Проінтегруємо ліву і праву частину рівняння (1) на кожному із проміжка

[ ] : .

При дуже малому кроці сітки вважатимемо значення функції на кожному із проміжків сталою тоді (4) запишемо як

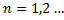(6) – метод Ейлора

Ми замінюємо інтегральну криву прямолінійним відрізком який виходить із точки . Геометрично метод полягає в заміні інтегральної кривої ламаною і кожна ланка цієї ламаної є прямолінійна і вона виходить з точки з кутовим коефіцієнтом . Таку ламану ще називають «Ламаною Ейлера». Недоліком є мала точність і систематичне накопичення похибки.

Вдосконалений метод Ейлера

Для побудови даного методу ми будемо обчислювати значення в деякій проміжній точці

Знайдемо значення функції

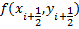
Тоді удосконалений метод Ейлера буде виглядати

Удосконалений метод Ейлера полягає в побудові Ламаної Ейлера, де на кожній ділянці [ ] ми заміняємо прямолінійним відрізком, який виходить із точки з кутовим коефіцієнтом

Метод Ейлера-Коші

В методі Ейлера-Коші замість ми будемо обраховувати середнє арифметичне

тоді одержимо формулу

метод Ейлера-Коші

Збіжність методу Ейлера

При розгляді чисельних методів головним питанням є питання збіжності. Стосовно різницевих методів, до яких відноситься метод Ейлера, важливим є поняття збіжності при . Для доведення збіжності ми будуємо послідовність сіток 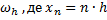таких що при . Будемо говорити що метод Ейлера збігається в точці , якщо тоді ж метод збігається на проміжку, якщо він збігається в кожній точці цього проміжку.

Кажуть, що метод має тий порядок точності, якщо , що виконується

.

Будемо говорити, що різницевий метод апроксимує дане диференціальне рівняння, якщо похибка прямує до нуля при .,також метод має -ий порядок апроксимації якщо похибка нескінченно мала того порядку.

Знайдемо оцінку похибки.

Припустимо є неперервною в області

і задовольняє умову Ліпшеца з сталою .

Також виконується

тоді розглянемо диференціальне рівняння тоді звичайний метод Ейлера буде виглядати:

Тоді позначимо похибку це похибка наближення до точного значення . Тоді за допомогою рівнянь виду (5) можемо записати рівняння для приросту похибки для рівняння

У рівнянні (6) враховуючи (4), можемо продовжити

У (7) про інтегруємо другий доданок по частинах

Підставимо одержаний вираз у (7) тоді

Врахувавши обмеження (2), а також умову Ліпшеца(1)

\

Врахувавши (5):

Розглянемо рівність (6):

Врахувавши (8’)

Таким чином (9) представляє собою рекурентну оцінку похибки на кроці через -тий крок. Розглянемо оцінку на –товім кроці.

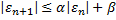
Тоді можемо записати

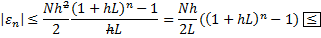
Використаємо рівність

Ми одержимо похибку де -величина проміжку а.

Як бачимо з формули оцінки похибки, Метод Ейлора має 1-й порядок апроксимації із зменшенням кроку похибка зменшується. Тому можемо зробити висновок, що на довільнім скінченнім проміжку при метод є збіжний, але недоліком цього методу є повільна збіжність.

Дослідимо метод Ейлера на стійкість.

Не завжди початкове наближення буде одержане точно, тобто замість ми будемо враховувати . - абсолютна похибка між точними і наближеними значеннями.

, тоді врахувавши метод Ейлера (4) можемо записати

Знайдемо абсолютну похибку враховуючи що функція задовольняє умову Ліпшица

…. …. ….

Тоді

…. .… .….

Із останньої нерівності випливає що похибка початкових даних не накопичується, тобто метод Ейлера має обчислювальну стійкість

Можемо сказати що похибка початкових даних не накопичується в методі Ейлера і метод має обчислювальну стійкість.

Методи Рунге-Кутта

Від метода Ейлера вони відрізняються порядком точності, а також тим, що в методі Ейлера не допускається обмеження правих частин 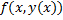не тільки в точках сітки, а і в деяких проміжних точках. Розглядається задача (1)-(2)

Нехай є шуканий розвязок задачі (1)-(2). Розкладемо в ряд Тейлора в околі точки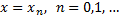

Взявши

Із (4):

Формула (4’) визначає розвязок в точці . де може бути визначене з рівняння (1) при

Обчислення коефіцієнта (4) представляє собою великий об’єм обчислень. Тоді Рунге запропонував обчислювати замість коефіцієнта суму

.

Тодірозвязок буде представлений і тоді з формули (5) шукатимемо наступне наближення . Будемо вважати що коефіцієнт будуть вибиратися від досягнення потрібної точності.

Сума коефіцієнтів .

!Зауважимо, що метод Рунга-Кута не використовується при

При - одержимо простий метод Ейлера

При

(

Розглянемо рівняння яке задовольняє похибка методу Ейлера

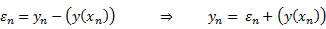
Праву частину рівняння (8) можна представити у вигляді суми двох доданків

Де функція називається нев`язковою або похибкою апроксимації рівняння (6) на розвязку задачі (1), (2). Нев’язка являє собою результат підставки точного розв’язку у різницеве рівняння

Якщо співпадатиме з точним розв’язком то нев’язка = 0. Тоді будемо говорити, що різницевий метод апроксимує початкове диференціальне рівняння (1). Якщо і різницевий метод буде мати тий порядок точності якщо .

Розглянемо різницевий метод (7) і підставимо коефіцієнти

Тоді за означенням похибки апроксимації або нев’язкою методу (7) будем називати функцію

Вираз (11) одержується заміною у (10) наближеного розв’язку точним розв’язком. Знайдемо порядок апроксимації із припущення що функція є достатньо гладкою. Для цього розкладемо праві доданки в (11) в околі точки в ряд Тейлора.

Розпишемо . Ці всі вирази підставимо у нев’язку

.

.

Формула (12) представляє собою нев’язку методу (7) і при метод буде мати перший порядок апроксимації, якщо ж додатково вимагати, що то ми одержимо метод другого порядку точності. Тим самим ми одержимо сім’ю методів Рунге-Кутта другого порядку і ці методи можуть бути записані у вигляді

1)

- метод Рунга-Кута 2-го порядку