
Числові розв’язки системи лінійних алгебраїчних рівнянь. Правило Крамера.
|
|
Числові розв’язки системи лінійних алгебраїчних рівнянь. Правило Крамера.
X1=  1/
1/  , X2=
, X2=  2/
2/  ,…, Xn=
,…, Xn=  n/
n/  , де
, де
 =
= 
 не дорівнює 0.
не дорівнює 0.
 1,
1,  2,….,
2,….,  n- визначники,які отримані з визначника системи заміною відповідних стовпців стовпцем вільних членів. Якщо
n- визначники,які отримані з визначника системи заміною відповідних стовпців стовпцем вільних членів. Якщо  =
=  1=
1=  2=…=
2=…=  n=0, то система має безліч розвязків. Матричний метод.
n=0, то система має безліч розвязків. Матричний метод.
А= 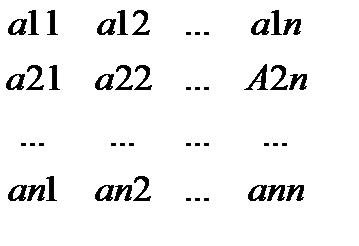 - матриця системи. В=
- матриця системи. В=  матриця вільних членів. Х=
матриця вільних членів. Х=  - матриця невідомих. Якщо детермінант не рівний 0 , то Х=
- матриця невідомих. Якщо детермінант не рівний 0 , то Х=  B
B
Метод Гауса.
Суть методу Гауса полягає в тому що задану слар зводять до еквівалентної їй системи шляхом послідовного вилучення невідомих так щоб одержати систему в якій одне зрівнянь має лише 1 невідому .Знайшовши цю невідому методом підстановки знаходимо значення решти невідомих.
1.2.Класифікація диференціальних рівнянь в частинних похідних.
Диференціальне рівняння з частинними похідними — диференціальне рівняння, що містить невідомі функції декількох змінних і їх частинні похідні.
Розрізняють звичайні диф. Рівняння і диф. Рівняння в частинних похідних.
Звичайні диференціальні рівняння — рівняння вигляду

де x = x(t) — невідома функція (можливо, вектор-функція; в такому випадку часто говорять про систему диференціальних рівнянь), що залежить від змінної t, штрих означає диференціювання по t. Число n називається порядком диференціального рівняння.
Диференціальним рівнянням з частинними похідними називається рівняння виду
 тобто це рівняння що містить невідомі функції від декількох змінних та їх частинних похідних.
тобто це рівняння що містить невідомі функції від декількох змінних та їх частинних похідних.
2.1..Мінор матриці. Алгебраїчне доповнення до елеметна  . Вираз для визначення матриці через його доповнення.
. Вираз для визначення матриці через його доповнення.
Мінором матриці A порядку k називається визначник матриці, утвореній елементами на перетині k стовпчиків та k рядків. Нехай дано матрицю розміром  . Оберемо в ній k стовпчиків та k рядків без повторів . Елементи, що знаходяться на перетині обраних рядків та стовпчиків утворюють матрицю порядку k. Визначник цієї матриці називається мінором порядку k заданої матриці. Алгебраїним доповненням
. Оберемо в ній k стовпчиків та k рядків без повторів . Елементи, що знаходяться на перетині обраних рядків та стовпчиків утворюють матрицю порядку k. Визначник цієї матриці називається мінором порядку k заданої матриці. Алгебраїним доповненням  елемента
елемента  називають мінор цього елемента, взятий зі знаком
називають мінор цього елемента, взятий зі знаком  тобто
тобто 
Для того шоб визначити визначник матриці через його доповнення потрібно :
1 Знайти алгебраїчні доповнення певного стовпця або рядка матриці.
2.Кожен елемент помножити на своє доповнення і додати по сумі певного рядка або стовпця.( сума або по рядку або по стовпці).
Інтегрування – лабораторна №6.
Интегрированиеи дифференцирование - самые простые, с вычислительной точки зрения, операции, реализованные в MathCAD в виде операторов. Тем не менее, если расчеты выполняются с помощью вычислительного процессора, необходимо хорошо представлять себе особенности численных алгоритмов, действие которых остается для пользователя "за кадром".
Интегрирование, дифференцирование, как и множество других математических действий, устроено в MathCAD по принципу "как пишется, так и вводится". Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus(Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш +<7> (или символа "&", что то же самое). Появится символ интеграла с несколькими местозаполнителями , в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования.
Можно вычислять интегралы с одним или обоими бесконечными пределами. Для этого на месте соответствующего предела введите символ бесконечности, воспользовавшись, например, той же самой панелью Calculus(Вычисления). Чтобы ввести -°° (минус бесконечность), добавьте знак минус к символу бесконечности, как к обычному числу.
Чтобы получить результат интегрирования, следует ввести знак равенства или символьного равенства. В первом случае интегрирование будет проведено численным методом, во втором - в случае успеха, будет найдено точное значение интеграла с помощью символьного процессора MathCAD.


Первая производная
Для того чтобы продифференцировать функцию f (х) в некоторой точке:
1. Определите точку х, в которой будет вычислена производная, например, х:=1.
2. Введите оператор дифференцирования нажатием кнопки Derivative(Производная) на панели Calculus(Вычисления) или введите с клавиатуры вопросительный знак .
3. В появившихся местозаполнителях введите функцию, зависящую от аргумента х, т. е. f (х), и имя самого аргумента х.
4. Введите оператор <=> численного или <- символьного вывода для получения ответа.

Не забывайте предварительно определять точку, в которой производится численное дифференцирование, как это сделано в первой строке листинга.
Конечно, можно, как и при использовании других операторов, предварительно определить функцию в отдельном выражении, а затем посчитать ее производную; или применить оператор дифференцирования для определения собственных функций пользователя.


Для численного дифференцирования MathCAD применяет довольно сложный алгоритм, вычисляющий производную с точностью до 7-8-го знака после запятой. Этот алгоритм (метод Риддера) описан во встроенной справочной системе MathCAD. Погрешность дифференцирования не зависит от констант TOL или CTOL, в противоположность большинству остальных численных методов, а определяется непосредственно алгоритмом.
Исключение составляют функции, которые дифференцируются в окрестности сингулярной точки; например для рассмотренной нами функции f(x)=l/x это будут точки вблизи х=0. При попытке найти ее производную при х=0 будет выдано сообщение об одной из ошибок деления на ноль "Can't divide by zero"(Деление на ноль невозможно) или "Found a singularity while evaluating this expression. You may be dividing by zero"(Найдена сингулярность при вычислении этого выражения. Возможно, вы делите на ноль) Если попробовать численно определить производную очень близко к нулю, например, при х=10100, то может появиться сообщение об ошибке "Can't converge to a solution"(Невозможно найти решение). Встретившись с одной из упомянутых ошибок, присмотритесь повнимательнее к дифференцируемой функции и убедитесь, что вы не имеете дело с точкой сингулярности.
4.1.Причини виникнення похибок обчислень та їх класифікація.
Основною проблемою чисельних методів є похибка.
Похибка вимірювання — це відхилення результату вимірювання від істинного значення вимірюваної фізичної величини .
Причини виннекнення похибок:
1.Вихідні дані є не точними.
2.Не точні методи обчислень .
3.В процесі обчислень проводяться заокруглення.
Абсолютна похибка— абсолютна різниця між результатом вимірювання та умовно істинним значенням вимірюваної величини.
Нехай a — абсолютне значення вимірювальної величини, b — її наближення. Тоді абсолютна похибка вимірювання ε визначається як
ε = | a − b |
Відносна похибка - це похибка вимірювання, виражена як відношення абсолютної похибки до дійсного чи виміряного значення.
Відносну похибку у долях вимірюваної величини або в процентах знаходять із співвідношень
 або
або 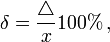
граничну абсолютну похибку  наближеного числа
наближеного числа  , рівну по можливості найменшому числу, що є більшим за абсолютну похибку
, рівну по можливості найменшому числу, що є більшим за абсолютну похибку  .
.
Значення  і
і  дозволяють вказати інтервал, що містить точне значення
дозволяють вказати інтервал, що містить точне значення  :
:  .
.
4.2.Інтерполяційний многочлен Лагранджа.
Інтерполяцій́ний многочле́н Лагра́нжа — многочлен мінімального степеня, що приймає дані значення у даному наборі точок.

















Приклад з 5 вузлами:
Лагранж предложил способ вычисления таких многочленов:

где базисные полиномы определяются по формуле:

5.1.Складання математичної таблиці для значень функції  . Реалізація методу складання математичної таблиці для значень функції
. Реалізація методу складання математичної таблиці для значень функції  в середовищі Mathcad, Matlab, Maple, Exel.
в середовищі Mathcad, Matlab, Maple, Exel.
Для виведення математичних таблиць використовують формулу Тейлора. Для цього потрібно розкласти функцію в ряд Тейлора. Нижче наведено приклад для функції sinx:



5.2.Проблеми вибору апроксимуючих функцій. Похибка апроксимації.
Апроксима́ція (лат. approximare — наближати) — наближене вираження одних математичних об'єктів іншими, простішими, напр. кривих ліній — ламаними, ірраціональних чисел — раціональними, неперервних функцій — многочленами і т. д
Однією із задач, які розв¢язує сучасна обчислювальна математика, є проблема наближення функції однієї змінної та багатьох дійсних змінних іншими функціями більш простої, взагалі кажучи будови, які легко обчислюються на електронно-обчислювальних машинах. Інша назва цієї задачі – апроксимування функції. Ця задача може постати, наприклад, у випадку, коли або функція задана своїми значеннями у вигляді таблиці результатів експерименту, або коли функція має складну аналітичну будову і знаходження її значення у деяких точках викликає обчислювальні труднощі. Так, зокрема, всі широко вживані на практиці функції sin(x), cos(x), exp(x), ln(x), ch(x), sh(x) та багато інших визначаються при обчисленнях на ЕОМ за допомогою функціональних рядів або ланцюгових дробів.
В останні роки різко зріс інтерес до класичних методів раціональної апроксимації функцій. Це пов¢язано з тим, що такі апроксимації знайшли різноманітне застосування в обчислювальних задачах теоретичної фізики та механіки.
Из курса математики известны 3 способа задания функциональных зависимостей:
аналитический
графический
табличный
Табличный способ обычно возникает в результате эксперемента.
Недостаток табличного задания функции заключается в том, что найдутся значения переменных которые неопределены таблицей. Для отыскания таких значений определяют приближающуюся к заданной функцию, называемой аппроксмирующей,а действие замены аппроксимацией.
| φ(х) |
φ(х)- аппроксимирующая функция.
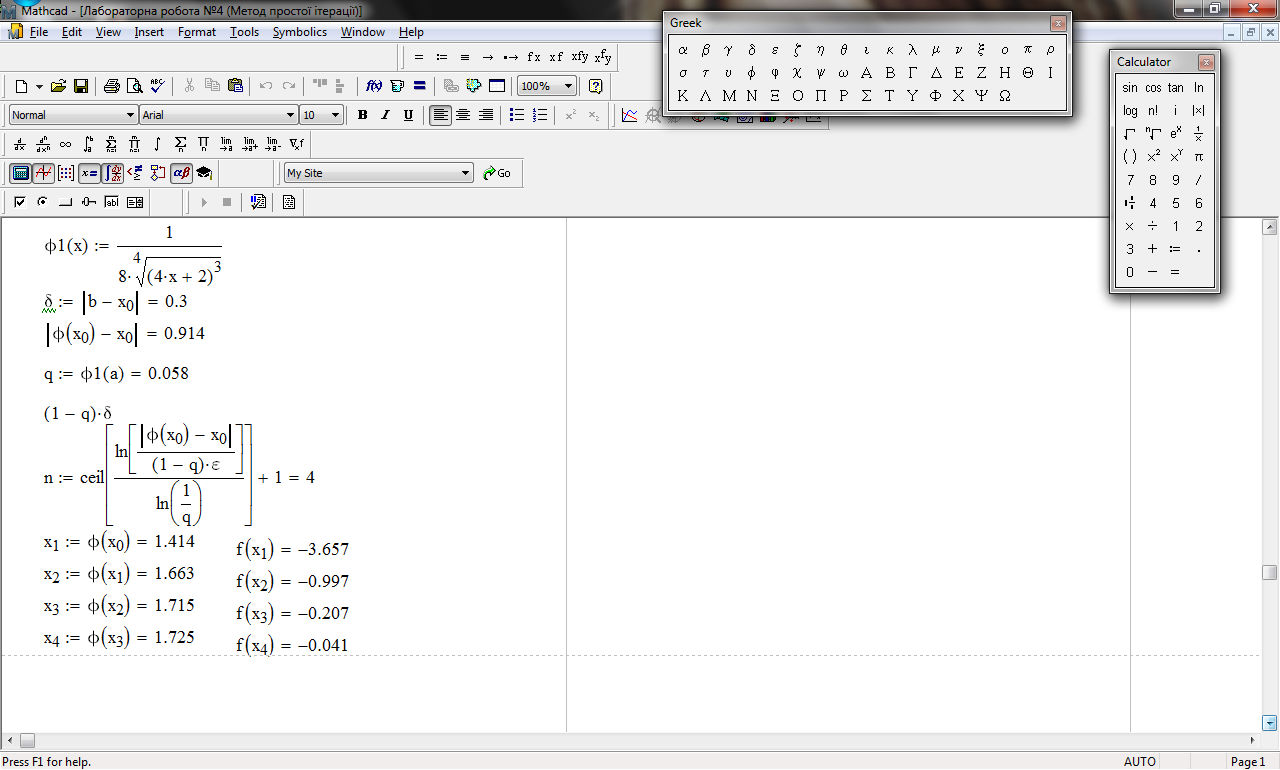
6.1.Метод січних (хорд) розв’язку (знаходження коренів) нелінійних рівнянь. Метод простих ітерацій. Приклад.
Метод січних
Однією з головних проблем при застосуванні методу Ньютона є необхідність аналітичного опису похідної. Якщо це складно чи неможливо, то можна застосувати її наближену оцінку (рисунок 2). Тоді замість методу дотичних застосовується метод січних, за яким  де
де  - наближена оцінка похідної, що розглядається як січна, а не як дотична, і може бути оцінена за формулою
- наближена оцінка похідної, що розглядається як січна, а не як дотична, і може бути оцінена за формулою  Чи
Чи  де h — деякий невеликий крок.
де h — деякий невеликий крок.
Алгоритм цього методу подібний методу Ньютона, але з іншою ітераційною формулою. 
Рис. 2. Метод січних Метод простої ітерації
Метод простої ітерації застосовується до розв’язування нелінійного рівняння виду  . (7) Перейти від рівняння (1) до рівняння(7) можна багатьма способами, наприклад, вибравши
. (7) Перейти від рівняння (1) до рівняння(7) можна багатьма способами, наприклад, вибравши  , де
, де  - довільна знакостала неперервна функція.
- довільна знакостала неперервна функція.
Вибравши нульове наближення x0, наступні наближення знаходяться за формулою  . (9) Наведемо достатні умови збіжності методу простої ітерації.
. (9) Наведемо достатні умови збіжності методу простої ітерації.
Теорема 1. Нехай для вибраного початкового наближення x0 на проміжку  (10) функція j(x) задовольняє умові Ліпшиця
(10) функція j(x) задовольняє умові Ліпшиця  (11) де 0<q<1, і виконується нерівність
(11) де 0<q<1, і виконується нерівність
 . (12) Тоді рівняння (7) має на проміжку S єдиний корінь
. (12) Тоді рівняння (7) має на проміжку S єдиний корінь 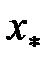 , до якого збігається послідовність (9), причому швидкість збіжності визначається нерівністю
, до якого збігається послідовність (9), причому швидкість збіжності визначається нерівністю 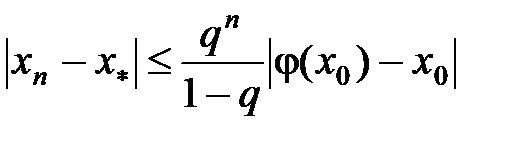 . (13)
. (13)
Зауваження: якщо функція j(x) має на проміжку S неперервну похідну  , яка задовольняє умові
, яка задовольняє умові  , то функція j(x) буде задовольняти умові (11) теореми 1.
, то функція j(x) буде задовольняти умові (11) теореми 1.
З (13) можна отримати оцінку кількості ітерацій. які потрібно провести для знаходження розв’язку задачі (7) з наперед заданою точністю e:
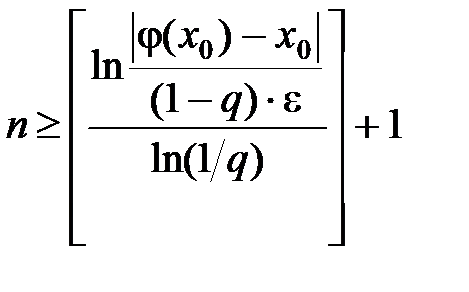 (15) Наведемо ще одну оцінку. що характеризує збіжність методу простої ітерації:
(15) Наведемо ще одну оцінку. що характеризує збіжність методу простої ітерації:  . (16)
. (16)


Визначення
Нехай маємо n значень xі, кожному з який відповідає своє значення yі. Потрібно знайти таку функцію F, що:

При цьому:
хі називають вузлами інтерполяції
пари (xі, yі) називають точками даних чи базовими точками
різницю між «сусідніми» значеннями xі-xі-1 — кроком
функцію F (x) — функцією, що інтерполює чи інтерполянтом.
Метод Гауса
Пусть исходная система выглядит следующим образом

Матрица A называется основной матрицей системы, b — столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно)
Для системы n линейных уравнений с n неизвестными (над произвольным полем)
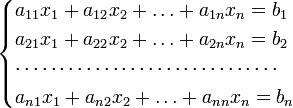
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,...,bn и x1,x2,...,xn, либо набор c1,c2,...,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Ма́тричный метод решения систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:
AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
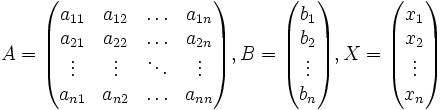
Умножим это матричное уравнение слева на A - 1 — матрицу, обратную к матрице A:  Так как A − 1A = E, получаем X = A - 1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
Так как A − 1A = E, получаем X = A - 1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: 
Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Итерационные методы
Метод Ньютона (метод касательных): Одномерный случай. Для того, чтобы решить уравнение  пользуясь методом простой итерации, необходимо привести его к виду
пользуясь методом простой итерации, необходимо привести его к виду  где
где  — сжимающее отображение. Чтобы отображение было наиболее эффективно, необходимо, чтобы в точке очередной итерации x * выполнялось
— сжимающее отображение. Чтобы отображение было наиболее эффективно, необходимо, чтобы в точке очередной итерации x * выполнялось 
удем искать решение данного уравнения в виде:

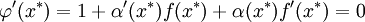
Воспользуемся тем, что  и получим окончательную формулу для
и получим окончательную формулу для 
 С учётом этого сжимающая функция примет вид:
С учётом этого сжимающая функция примет вид: 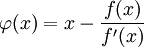 Тогда алгоритм нахождения численного решения уравнения
Тогда алгоритм нахождения численного решения уравнения  сводится к итерационной процедуре вычисления:
сводится к итерационной процедуре вычисления: 
Метод релаксации
Материал из Википедии — свободной энциклопедии
Метод релаксации - приближённый метод решения систем линейных уравнений.
Система линейных уравнений 
приводится к виду 
где 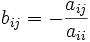 ,
, 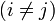 ,
,  Находятся невязки Rj:
Находятся невязки Rj:
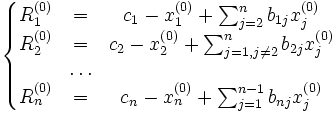
Выбирается начальное приближение X(0) = 0. На каждом шаге необходимо обратить в ноль максимальную невязку: 
Условие остановки: 
Ответ находится по формуле: 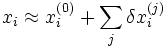
Постановка задачі чисельного диференціювання. Найпростіші формули числового диференціювання: різницева, центральна різницева та друга різницева похідні. Похибки різницевої, центральної різницевої та другої різницевої похідних.

Обернена матриця. Приклад.

Метод прямокутників
Найпростішим методом чисельного інтегрування є метод прямокутників. В ньому здійснюється заміна означеного інтеграла інтегральною сумою. За точки  можуть вибиратися ліві (
можуть вибиратися ліві (  ) або праві (
) або праві (  ) границі елементарних відрізків. Позначивши
) границі елементарних відрізків. Позначивши  ,
,  , отримаємо наступні формули метода прямокутників відповідно до цих двох випадків:
, отримаємо наступні формули метода прямокутників відповідно до цих двох випадків:
 , (5)
, (5)  . (6)
. (6)
Широко поширеним та найбільш точним є вигляд формули прямокутників, що використовує значення функції в середніх точках елементарних відрізків (метод середніх прямокутників):
 , (7)
, (7) 
Метод трапеційМетод трапецій використовує лінійну інтерполяцію, тобто графік функції  подається у вигляді ламаної, що з’єднує точки
подається у вигляді ламаної, що з’єднує точки  . В цьому випадку площа всієї фігури (криволінійної трапеції) складається з площ елементарних прямолінійних трапецій. Площа кожної такої трапеції рівна:
. В цьому випадку площа всієї фігури (криволінійної трапеції) складається з площ елементарних прямолінійних трапецій. Площа кожної такої трапеції рівна:  . Додаючи всі ці рівності, отримуємо формулу трапецій для чисельного інтегрування:
. Додаючи всі ці рівності, отримуємо формулу трапецій для чисельного інтегрування:
 . (8) Важливим частинним випадком розглянутих формул є їх застосування при чисельному інтегруванні з постійним кроком
. (8) Важливим частинним випадком розглянутих формул є їх застосування при чисельному інтегруванні з постійним кроком  (
(  ). Формули прямокутників і трапецій в цьому випадку приймають відповідно вигляд
). Формули прямокутників і трапецій в цьому випадку приймають відповідно вигляд
 (9)
(9)  (10)
(10)
Метод парабол (метод Сімпсона)
Розіб’ємо відрізок інтегрування  на парне число рівних частин з кроком
на парне число рівних частин з кроком  . На кожному відрізку
. На кожному відрізку  ,
,  , ... ,
, ... ,  , ... ,
, ... ,  підінтегральну функцію
підінтегральну функцію  замінимо інтерполяційним многочленом другого степеня:
замінимо інтерполяційним многочленом другого степеня:
 .
.
Коефіцієнти цих квадратних тричленів можуть бути знайдені з умов рівності многочлена в точках  відповідним табличним даним
відповідним табличним даним  . За
. За  можна прийняти інтерполяційний многочлен Лагранжа другого степеня, що проходить через точки
можна прийняти інтерполяційний многочлен Лагранжа другого степеня, що проходить через точки  ,
,  ,
,  :
:
 .
.
Елементарна площа  може бути знайдена за допомогою означеного інтеграла. Враховуючи рівність
може бути знайдена за допомогою означеного інтеграла. Враховуючи рівність  , отримаємо
, отримаємо

 .
.
Провівши такі розрахунки для кожного елементарного відрізку  , просумуємо отримані вирази:
, просумуємо отримані вирази:
 .
.
Дані вирази для  приймається за значення означеного інтегралу:
приймається за значення означеного інтегралу:
 . (11)
. (11)
Отримане співвідношення називається формулою Сімпсона.
1 1.Числові розв’язки системи лінійних алгебраїчних рівнянь. Правило Крамера.
2.Класифікація диференціальних рівнянь в частинних похідних.
2 1.Мінор матриці. Алгебраїчне доповнення до елеметна  . Вираз для визначення матриці через його доповнення.
. Вираз для визначення матриці через його доповнення.
2.Диференціальне рівняння для коливних процесів в акустині, електродинаміці та для встановлених процесів (на прикладі поля електричного поля).
3 1.Ряд Тейлора для функції багатьох змінних та його роль в чисельних методах. Приклад. Похибки функцій багатьох змінних на основі її ряду Тейлора. Приклад.
2.Реалізація методів чисельного диференціювання та інтегрування в середовищі Mathcad, Matlab, Maple, Exel.
4 1.Причини виникнення похибок обчислень та їх класифікація.
2.Інтерполяційний многочлен Лагранджа.
5 1.Складання математичної таблиці для значень функції  . Реалізація методу складання математичної таблиці для значень функції
. Реалізація методу складання математичної таблиці для значень функції  в середовищі Mathcad, Matlab, Maple, Exel.
в середовищі Mathcad, Matlab, Maple, Exel.
2.Проблеми вибору апроксимуючих функцій. Похибка апроксимації.
6 1.Метод січних (хорд) розв’язку (знаходження коренів) нелінійних рівнянь. Метод простих ітерацій. Приклад.
2.Метод сіток для рівнянь диференціального рівняння в частинних похідних параболічного типу (на прикладі рівняння теплопровідності).
7 1.Задачі наближення функцій (експеремнтальних даних) та використання результатів наближень.
2.Поняття про числові методи математичної статистики.
8 1.Формула ейлера та її розв’язок з розкладами в ряди функцій sinx та cjsx.
2.Використання в задачах диференціювання інтерполяційних многочленів.
9 1.Метод половинного ділення в задачі уточнення кореня нелінійного рівняння. Абсолютна похибка методу.
2.Початкові та граничні умови для рівнянь в частинних похідних (на прикладі рівняння теплопровідності).
10 1.Визначник (детермінант) матриці, алгоритм його обчислення.
2.Вивід диференціального рівняння теплопровідності.
11 1.Матриця. Основні види матриць. Транспонована матриця, рівні матриці. Основні дії над матрицями.
2.Побудова диференціального рівняння для математичного маятника та для маятника поперечних коливань.
12 1.Предмет «Чисельні методи», його роль в сучасній науці.
2.Загальна постановка задачі інтерполяції. Сітка, рівномірна сітка, вузли інтерполяції. Інтерполяційний поліном.
13 1.Значущі цифри числа, вірні значущі цифри, точність числа до  . Заокруглення числа.
. Заокруглення числа.
2.Сплайн-інтерполяції. Поліноміальний сплайн.
14 1.РядМаклорена для функцій sinx та cosx.
2.Реалізація методів наближень (інтерполяція та апроксимація) в середовищі Mathcad, Matlab, Maple, Exel.
15 1.Основні задачі числових методів алгебри.
2.Диференціальні рівняння як моделі реальних явищ, процесів. Побудова диференціального рівняння для радіоактивного розпаду.
16 1.Постановка задачі та етапи числових методів розв’язку нелінійних рівнянь (знаходження коренів нелінійних рівнянь).
2.Різницевий метод розв’язку крайової задачі для лінійного звичайного диференціального рівняння другого порядку.
17 1.Метод Гауса розв’язків системи лінійних алгебраїчних рівнянь. Реалізація методів знаходження розв’язків системи лінійних алгебраїчних рівнянь в середовищі Mathcad, Matlab, Maple, Exel.
2.Задача Коші та крайові задачі для звичайних диференціальних рівнянь. Поняття про аналітичні методи розв’язку звичайних диференціальних рівнянь. Приклади.
18 1.РядМаклорена для функції однієї змінної. Приклад розкладу в ряд для функції  .
.
2.Апроксимція функції. Метод найменших квадратів і його використання в задачах апроксимації.
19 1.Знаходження коренів функції багатьох змінних: градієнтний метод.
2.Метод сіток для рівнянь диференціального рівняння в частинних похідних еліптичного типу (на прикладі рівняння двох змінних).
20 1.Способи відділення коренів нелінійних рівнянь.
2.Реалізація числових методів розв’язку звичайних диференціальних рівнянь в середовищі Mathcad, Matlab, Maple, Exel.
21 1.Реалізація методів лінійної алгебри в середовищі Mathcad, Matlab, Maple, Exel.
2.Задача Коші та крайова задача для рівняння першого порядку та їх розв’язок різницевим методом.
22 1.Метод Ньютона розв’язку (знаходження коренів) нелінійних рівнянь. Спрощений метод Ньютона.
2.Наближені методи розв’язку крайових задач: метод коллокацій, метод найменших квадратів.
23 1.Реалізація методів знаходження коренів функцій однієї і багатьох змінних в середовищі Mathcad, Matlab, Maple, Exel.
2.Реалізація методів чисельного розв’язку диференціальних рівнянь в частинних похідних в середовищі Mathcad, Matlab, Maple, Exel.
24 1.Ряд Тейлора для функції однієї змінної на основі її ряду Тейлора. Приклад.
2.Постановка задачі чисельного інтегрування функцій. Квадратурні формули прямокутників, трапецій, Симсона. Похибки чисельного інтегрування.
25 1.Складання математичної таблиці для значень функцій sinx та cosx. Реалізація методу складання математичних таблиць для значень функцій sinx та cosx в середовищі Mathcad, Matlab, Maple, Exel.
2.Постановка задачі чисельного диференціювання. Найпростіші формули числового диференціювання: різницева, центральна різницева та друга різницева похідні. Похибки різницевої, центральної різницевої та другої різницевої похідних.
26 1.Чисельний метод знаходження числа пі.
2.Поліномний кубічний сплайн. Похибка наближення поліноміальними сплайнами.
27 1.Обернена матриця. Приклад.
2.Класифікація диференціальних рівнянь.
28 1.Ряд Тейлора для функції двох змінних та його роль в чисельних методах. Приклад. Похибка функції двох змінних на основі її ряду Тейлора. Приклад.
2.Метод Монте-Карло обчислення інтегралів.
29 1.Похибка числа, абсолютна і відносна похибки, гранична абсолютна похибки.
2.Скінченні та розділені різниці. Інтерполяційний многочлен Ньютона. Похибка інтерполяції.
30 1.Реалізація числових методів знаходження коренів нелінійних рівнянь в середовищі Mathcad, Matlab, Maple, Exel.
2.Метод сіток для рівнянь диференціального рівняння в частинних похідних гіперболічного типу (на прикладі рівнянь двох змінних).
Числові розв’язки системи лінійних алгебраїчних рівнянь. Правило Крамера.
X1=  1/
1/  , X2=
, X2=  2/
2/  ,…, Xn=
,…, Xn=  n/
n/  , де
, де
 =
= 
 не дорівнює 0.
не дорівнює 0.
 1,
1,  2,….,
2,….,  n- визначники,які отримані з визначника системи заміною відповідних стовпців стовпцем вільних членів. Якщо
n- визначники,які отримані з визначника системи заміною відповідних стовпців стовпцем вільних членів. Якщо  =
=  1=
1=  2=…=
2=…=  n=0, то система має безліч розвязків. Матричний метод.
n=0, то система має безліч розвязків. Матричний метод.
А= 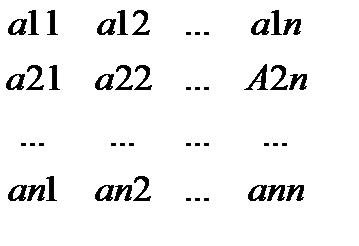 - матриця системи. В=
- матриця системи. В=  матриця вільних членів. Х=
матриця вільних членів. Х=  - матриця невідомих. Якщо детермінант не рівний 0 , то Х=
- матриця невідомих. Якщо детермінант не рівний 0 , то Х=  B
B
Метод Гауса.
Суть методу Гауса полягає в тому що задану слар зводять до еквівалентної їй системи шляхом послідовного вилучення невідомих так щоб одержати систему в якій одне зрівнянь має лише 1 невідому .Знайшовши цю невідому методом підстановки знаходимо значення решти невідомих.
1.2.Класифікація диференціальних рівнянь в частинних похідних.
Диференціальне рівняння з частинними похідними — диференціальне рівняння, що містить невідомі функції декількох змінних і їх частинні похідні.
Розрізняють звичайні диф. Рівняння і диф. Рівняння в частинних похідних.
Звичайні диференціальні рівняння — рівняння вигляду

де x = x(t) — невідома функція (можливо, вектор-функція; в такому випадку часто говорять про систему диференціальних рівнянь), що залежить від змінної t, штрих означає диференціювання по t. Число n називається порядком диференціального рівняння.
Диференціальним рівнянням з частинними похідними називається рівняння виду
 тобто це рівняння що містить невідомі функції від декількох змінних та їх частинних похідних.
тобто це рівняння що містить невідомі функції від декількох змінних та їх частинних похідних.
2.1..Мінор матриці. Алгебраїчне доповнення до елеметна  . Вираз для визначення матриці через його доповнення.
. Вираз для визначення матриці через його доповнення.
Мінором матриці A порядку k називається визначник матриці, утвореній елементами на перетині k стовпчиків та k рядків. Нехай дано матрицю розміром  . Оберемо в ній k стовпчиків
. Оберемо в ній k стовпчиків
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |