
Диференціальні рівняння із змінними, що розділяються
|
|
Диф рівнянням називається рівняння із змінними, що розділяються, якщо має наступні вигляд : y'= f(x)  f(y)
f(y)  (1)
(1)
Для даного рівняння завдання Коші про існування і єдиність рішення наступна : Якщо функція f(x)  безперервна в інтервалі (а;b), функція f(x)
безперервна в інтервалі (а;b), функція f(x)  і її похідна по у безперервна в інтервалі (з;d), то для будь-яких початкових даних хе
і її похідна по у безперервна в інтервалі (з;d), то для будь-яких початкових даних хе  (а;b), yе
(а;b), yе  (з;d), у=ц(х) рівняння (1), що задовольняє початковій умові ц(x)=
(з;d), у=ц(х) рівняння (1), що задовольняє початковій умові ц(x)=  ц
ц
Рівняння вигляду 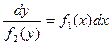 називається рівняння з роздільними змінними.
називається рівняння з роздільними змінними.
При рішенні рівнянь із змінними, що розділяються, виконати наступне:
1. Розділити змінні.
2. Інтегрований почленно отримане рівняння і знаходимо його загальне рішення.
3. Знайти приватне рішення, що задовольняє початковим умовам (якщо це не потрібно)
Диф рівняння типу M(x)dx + N(g)dy=0 або dy(f(y)=  f(x)
f(x)  dx -
dx -
називають рівнянням з відокремленими змінними.
Загальне рішення має вигляд: 
Приклад 1. Знайти загальне рішення рівняння xdx+ydy=0,интегрируем і отримуємо  т.к ліва частина ненегативна, то і права теж ненегативна. Хай 2С= С, тоді отримаємо x+y=с
т.к ліва частина ненегативна, то і права теж ненегативна. Хай 2С= С, тоді отримаємо x+y=с  .
.
Це рівняння сімейства концентричних кіл з центром на початку координат і радіусом С..
Рівняння виду M(x)  N(y)
N(y)  dx+M(x)
dx+M(x)  N(y)
N(y)  dy=0 називається рівнянням із змінними, що розділяються. Воно може бути приведене до рівняння з розділеними змінними шляхом ділення двох його частин на вираз
dy=0 називається рівнянням із змінними, що розділяються. Воно може бути приведене до рівняння з розділеними змінними шляхом ділення двох його частин на вираз
 N(x) M(y):
N(x) M(y):
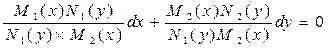
або

Приклад 2. Знайти загальне рішення рівняння
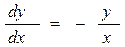 ;
;  інтегруємо
інтегруємо

In(y)=-In(x)+In(c) або In(y)= In 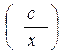
Загальне рішення y=c/x
Приклад 3. Знайти загальне рішення (1+x)ydx+(1-у)xdy= 0
 ;
;  ;
;

In (x) +x + In (y)-y=C або In (xy) +x-y = C - загальне рішення
Приклад 4.Знайти загальне рішення 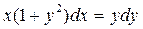 .
.
Розділимо змінні, маємо  , інтегруємо рівняння:
, інтегруємо рівняння: 
 .
.
Довільна стала С не може приймати будь – які числові значення , тому для подальшої зручності при перетвореннях замість С напишемо  . Маємо
. Маємо 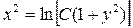 - загальний розв’язок даного рівняння.
- загальний розв’язок даного рівняння.
Приклад 5.Знайти часний розв’язок рівняння  , задовольняючи початковим умовам S= 4, при t= π ∕3.
, задовольняючи початковим умовам S= 4, при t= π ∕3.

 Це загальний розв’язок.
Це загальний розв’язок.
Для знаходження значення С , підставимо значення  у вираз для загального розв’язку:
у вираз для загального розв’язку:  , або
, або 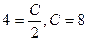 .
.
Часний розв’язок має вигляд  .
.
Приклад 6.Знайти загальне рішення

Приклад 7.Знайти загальне рішення

Приклад 8.Знайти загальне рішення

Приклад 9.Знайти загальне рішення.

Приклад 10.Знайти загальне рішення

Приклад 11.

Приклад 12.Знайти часний розв’язок рівняння

Приклад 13.
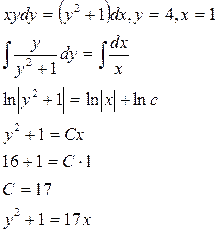
Приклад 14.

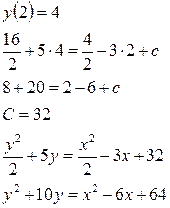
Лекція №2 Лінійні однорідні диференціальні рівняння першого порядку.
Мета: Узагальнити та систематизувати знання студентів про диференціальні рівняння першого порядку, однорідні диференціальні рівняння.
Сформувати вміння розв’язувати задачі, що передбачають використання диференціальних рівнянь, використання поняття інтегралів.
План вивчення теми.
1. Загальний вид лінійного диференціального рівняння.
2. Розв’язування прикладів.
Домашне завдання: індивідуальні завдання.
Загальний вид такого рівняння 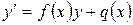 , (1)
, (1)
де  и
и 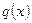 - завданні функції от
- завданні функції от 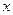 . Це рівняння лінійне відносно функції y(x) та її похідної.
. Це рівняння лінійне відносно функції y(x) та її похідної.
Якщо 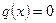 , то лінійне диференціальне рівняння (1) називається однорідним. Воно має вид
, то лінійне диференціальне рівняння (1) називається однорідним. Воно має вид 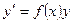 та розв’язується методом відокремлювання змінних:
та розв’язується методом відокремлювання змінних:
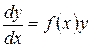 ,
, 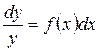 ,
,
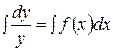 ,
, 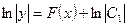 ,
,
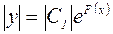 ,
, 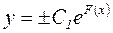 ,
, 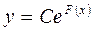 ,
,
де 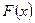 - будь-яка первісна функція
- будь-яка первісна функція  , а
, а 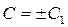 - деяка стала.
- деяка стала.
Якщо 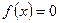 , то рівняння(1) має вид
, то рівняння(1) має вид 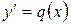 та розв’язується методом відокремлювання змінних:
та розв’язується методом відокремлювання змінних:
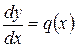 ,
, 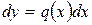 ,
,  ,
,
де 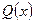 - будь-яка первісна функція
- будь-яка первісна функція 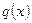 , а
, а  - деяка стала.
- деяка стала.
Приклад №1Знайти загальний розв’язок диференціального рівняння
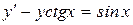 .
.
Розв’язання. Дане рівняння являється лінійним. Заміна  , тоді
, тоді 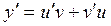 та рівняння перетворюється до виду
та рівняння перетворюється до виду
 , або
, або 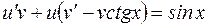 .
.
Розв’язуємо рівняння  та
та  .
.
Розв’язуємо рівняння :  ; маємо
; маємо
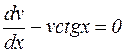 ,
,  ,
, 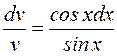 ,
, 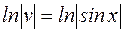 ,
,  .
.
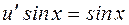 ,
,  ,
,  ,
, 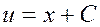 .
.
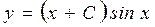 .
.
Приклад №2.Знайти загальний розв’язок диференціального рівняння
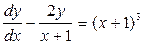 .
.
Розв’язання: Це лінійне рівняння: 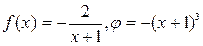 . Заміна
. Заміна 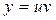 , тоді
, тоді 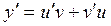 ,
,  . Рівняння перетворюється до виду:
. Рівняння перетворюється до виду: 
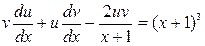 , або
, або 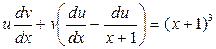 . (**)
. (**)
 .
.
Розділимо в цьому рівнянні змінні та про інтегруємо, маємо 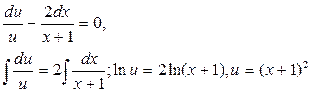
Підставляємо тепер вираз для U в рівняння (**), тоді отримуємо рівняння 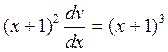 , або
, або 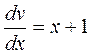 . Знаходимо
. Знаходимо 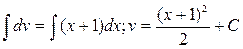 .
.
Получаємо загальний розв’язок даного рівняння: 
Пример№3.Знайти часний розв’язок диференціального рівняння
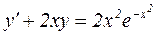 ,
, 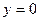 при
при 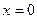 .
.
Розв’язання. Дане рівняння являється лінійним. Заміна 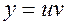 ; тоді
; тоді 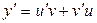 та рівняння перетворюється до виду
та рівняння перетворюється до виду
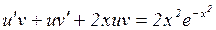 ,
, 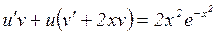 . (*)
. (*)
Положив  ; тоді
; тоді
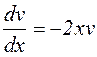 ,
,  .
.  , або
, або 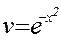 .
.
При 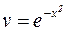 рівняння(*) має вид
рівняння(*) має вид 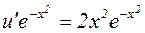 ,
, 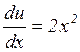 ,
,
 ,
, 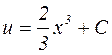 .
.
Знайти загальний розв’язок диференціального рівняння:
 .
.
Підставив в це рівняння начальні умови , получимо  ,
, 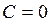 .
.
Часний розв’язок диференціального рівняння має вид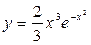 .
.
Пример№4.Знайти часний розв’язок диференціального рівняння  , якщо у=1 при х=0.
, якщо у=1 при х=0.
Розв’язання. Розділимо всі члени даного рівняння на 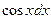 , маємо
, маємо 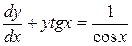 , яке є лінійним . Заміна
, яке є лінійним . Заміна 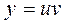 , тоді
, тоді 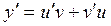 ,
, 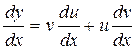 . Підставимо все в рівняння, та маємо
. Підставимо все в рівняння, та маємо 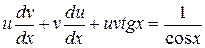 , або
, або 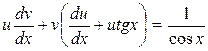 (***)
(***)
Отримуємо рівняння 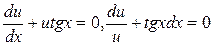 ,
,  . Підставляємо вираз в рівняння (***), та маємо
. Підставляємо вираз в рівняння (***), та маємо  , або
, або 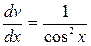 , тобто
, тобто 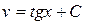 .
.
Загальний розв’язок записуємо так: 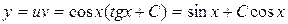 .
.
Маємо у=1, х=0, тому 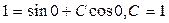 .
.
Часний розв’язок має вигляд: 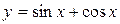 .
.
Приклади.
1. 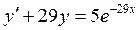
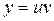
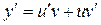
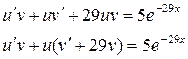
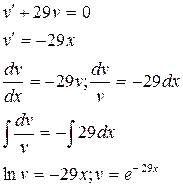
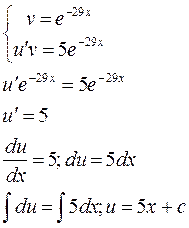
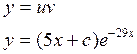
2. 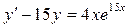
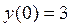
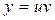 ;
; 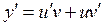 ;
; 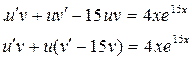
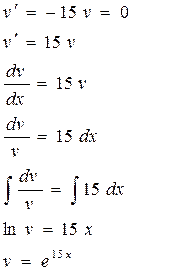
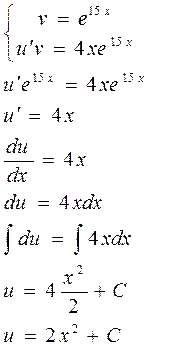
Підставляємо вираз в рівняння
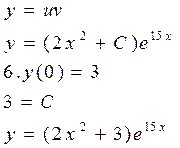
3. 
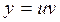

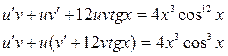
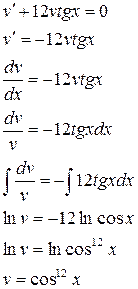

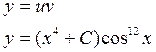 .
.
4. 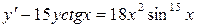
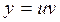
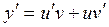
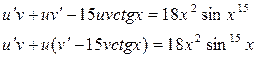



5. 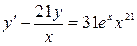
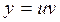

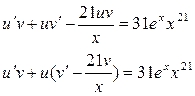
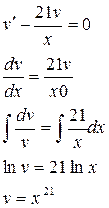
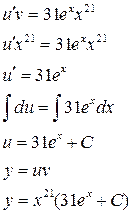 .
.
6. 
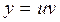


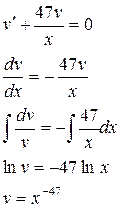
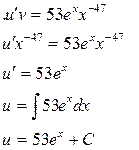
Загальний розв’язок : 
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |