Введемо для спрощення нові змінні

Тоді

Легко перевірити, що всі перші похідні від при дорівнюють нулю, тобто відповідно з (8.2) функція, коректована за Баттервортом максимально плоска.

Знайдемо положення полюсів функції, коректованої за Баттервортом. Для цього необхідно розв'язати рівняння Як комплексне число, S можна подати у вигляді модуля та аргумента. У даному випадку модуль дорівнює одиниці, тоді

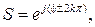
де k – будь–яке ціле число. Отже, розв'язок рішення для полюсів залежно від знака рівняння має вигляд:

- якщо n – непарне,

- якщо n – парне,

(8.6)

Таким чином, усі полюси функції коректованої за Баттевортом, знаходяться на колі одиничного радіуса поділеного однаковими кутовими відстанями, рис. 8.2 (а).

Рисунок 8.2 – Карти полюсів

Вони знаходяться як у лівій, так і у правій напівплощині комплексної змінної. Але необхідно мати на увазі, що аналізована функція є не функцією коефіцієнта передачі , а квадратом її "модуля"

Отже, необхідну карту полюсів функції можна дістати з
рис. 8.2, а, якщо виключити з неї полюси, що належать до і лежать у правій напівплощині.

Здобуті таким чином карти полюсів для зображені на рис. 8.2, б, в, г. Щоб перейти від нормованої частоти до звичайної необхідно масштаб на рис. 8.2 поділити на нормувальний множник Отже, всі корені лежать на колі з радіусом Цей радіус визначає значення граничної частоти , якщо її знаходити за рівнем послаблення –3дБ.

Використовуючи (8.6) та враховуючи полюси, що знаходяться тільки у лівій напівплощині, можна дістати аналітичний запис функції коректованої за Баттервортом

Коефіцієнти знаходяться, розкриваючи дужки та об'єднуючи члени однакових степенів S. Їх також можна здобути аналітично, якщо скористуватися рівняннями

де

У випадку корекції частотних чи фазових характеристик за Брауде нуль–полюсна карта показує оптимальне положення не тільки полюсів, а й нулів.

Щоб з'ясувати це оптимальне положення, розглянемо коефіцієнт передачі, використовуючи його нулі та полюси

(8.7)

де – нулі функції а – її полюси.

Припустимо, що всі полюси знаходяться на дійсній осі. Модуль коефіцієнта передачі можна подати у вигляді добутку частотних характеристик, що відповідають кожному полюсу. Якщо не враховувати нулі , тоді маємо

На рис. 8.3, а пунктирною прямою показані складові логарифмічної характеристики, що обумовлені кожним з полюсів, суцільною прямою – результувальна частотна характеристика.

Рисунок 8.3 – Логарифмічні амплітудно-частотні характеристики

З рис. 8.3, а можна бачити, що смуга пропускання практично визначається положенням найближчого до уявної осі полюса Отже, якщо в системі можна здійснити корекцію, яка створить окремий нуль то для ефективної корекції його необхідно розмістити там же де, і полюс тобто сумістити полюс з нулем , рис. 8.3, б. Суміщення його, наприклад, з полюсом практично не розширить смуги, а тільки зменшить падіння частотної характеристики у межах від до . Якщо застосовуючи корекцію можна одержати два нулі – та – то ними, як можна бачити з
рис. 8.3, б, необхідно компенсувати два найближчих до уявної осі полюси та Компенсація елементами корекції всіх полюсів неможлива, оскільки призводить до системи з фізично недосяжною необмеженою смугою пропускання.

На рис. 8.4, а показано випадок положення полюсів для оптимальної корекції.

Рисунок 8.4 – Положення полюсів на комплексній площині для випадку оптимальної корекції

У цьому випадку необхідно, у першу чергу, сумістити нулі з полюсами, найближчими до уявної осі, і, якщо полюси комплексні, тоді і компенсувальні нулі виявляються також комплексними. При компенсації полюсів нулями відповідні пари нулів та полюсів у виразі (8.7) скорочуються, і вираз для частотної характеристики спрощується.

Оптимальне положення нулів та полюсів на рис. 8.4, а відповідає системі мінімально–фазового типу, бо всі особливі точки розміщені в лівій напівплощині.

Здійснюючи корекцію iз залученням немінімально–фазових ланок, одержимо положення нулів та полюсів, що показані на рис. 8.4, б. У цьому випадку нулі, що корегують характеристику, як і раніше мають однакові з полюсами дійсні та уявні частини, але знак останніх для нулів додатний. Використовуючи такі ланки, можна здобути ідеальну частотну характеристику у широкому діапазоні частот. Фазовий зсув у такій ідеально–коригованій системі лишається залежним від частоти, тому включення подібних ланок у тракт підсилення, не змінюючи його частотних властивостей, дозволяє змінити його фазову характеристику. Такі ланки називають фазовими коректорами.

Розглянемо випадок, коли система має два комлексно–поєднаних полюси, а корекція можлива тільки з використанням одного нуля. У цьому випадку

де

Для спрощення подальших записів пропонується зміна р та введення замість неї змінно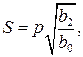ї тоді

де , a та – полюси

Розв'язуючи рівняння знаходимо полюси

При полюси комплексно–поєднані. Тоді

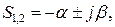
де Модуль коренів тобто при будь-яких значеннях полюси лежать на колі з одиничним радіусом, рис. 8.5, а.

Модуль частотної характеристики знаходиться після заміни S на

Рисунок 8.5 – Зображення полюсів

Згідно з умовою Брауде кореція має місце при або У цьому випадку може бути отримана частотна характеристика без підіймання з максимальною шириною смуги

Якщо прирівняти цей вираз до можна знайти максимальну граничну частоту

Вона однозначно визначається можливою величиною 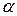при такому положенні нуля Зв'язок між та що відповідає умовам корекції Брауде, має вигляд

Числові значення та 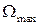наведені у табл. 8.1.

Таблиця 8.1 – Числові оптимальні значення коефіцієнтів та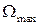

	0,707	0,900		1,19	1,55	2,0	5,0	0,707
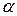
	1,0	0,900	0,865	0,82	0,775	0,75	0,715	0,707
		0,440	0,500	0,575	0,631	0,663	0,700	1,00
	1,55	1,34	1,27	1,19	1,11	1,07	1,01

Якщо нуль знаходиться у нескінченності, корекція за Брауде збігається з корекцією за Баттервортом. Обидва полюси при цьому розміщені на колі під кутом і знаходяться один від одного на кутовій відстані
(рис. 8.2, б та рис. 8.5, а).

Якщо їх розташувати праворуч (відносно рис. 8.5, а), то частотна характеристика виявиться вже не максимально плоскою і на ній з'явиться нерівномірність у вигляді підйому. Якщо їх розташувати ліворуч (у межах заштрихованого сектора), то характеристики, не будучи максимально плоскими, лишаться монотонними. Поява кінцевого нуля на дійсній осі зменшує кут розташування полюсів, у межах якого зберігається монотонність частотних характеристик (заштрихований сектор на рис. 8.5, б). Конкретні співвідношення між можливими положеннями полюсів і нулів подані у табл. 8.1.

Останній рядок таблиці дозволяє будувати логарифмічні частотні характеристики, використовуючи значення 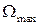як точки на осі частот, після якої вони одержують нахил – 12 дБ/окт.

Усе розглянуте стосується так званої високочастотної корекції, коли внаслідок її дії смуга пропускання збільшується у бік високих частот. Часто виникає необхідність покращити частотну характеристику у області нижніх частот, тобто розширити смугу пропускання у такий спосіб, щоб пристрій ефективно підсилював низькі частоти.

Корекція, що розширює смугу пропускання в область більш низьких частот чи покращувальна характеристика у цій області, зветься низькочастотною. Частотна характеристика для області нижніх частот

має такі особливості: отже поліноми та повинні мати однакові коефіцієнти при найвищих степенях і ці степені повинні бути однаковими: отже, поліном не повинен містити постійного члена. Тоді

Проведемо інверсію частоти та введемо нову частоту Потім поділивши чисельник та знаменник на дістанемо

Ця форма запису характеристики тотожна тій, що розглянута вище. Отже, до неї застосовується все те, що раніше було запропоновано до ВЧ корекції. Розширення смуги пропускання, тобто збільшення 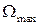у цьому випадку буде в дійсності означати розширення смуги пропускання у бік нижніх частот (зниження ). У такий спосіб "інверсією частоти" користуються не тільки при аналізі схем НЧ корекції, але і при їх синтезі.