
Задача про максимальну течію в мережі
|
|
Означення.
1 Розбивальна множина зв’язного графа – це така множина його ребер, вилучення яких призводить до незв’язного графа.
2 Розрізом називається така розбивальна множина, для якої ніяка власна підмножина не є розбивальною множиною.
Наприклад. Маємо граф

Розглянемо такі розбивальні множини його ребер:
1) {u1, u2, u5};
2) {u3, u6, u7, u8};
3) {u1, u2}.
З цих розбивальних множин розрізом будуть лише {u1, u2} і {u3, u6, u7, u8}.
Розглянемо орієнтований граф, де вага дуги сij > 0 – це пропускна спроможність дуги.
Пропускна спроможність розрізу – це сума пропускних спроможностей дуг, що утворюють розріз.
Мінімальний розріз – це розріз з мінімальною пропускною спроможністю.
Приклад. Маємо орієнтований граф

Розглянемо декілька розрізів цього графа і обчислимо пропускні спроможності цих розрізів.
Розріз R1: (1,4), (2,4), (3,4)
с14=1 с24= 4 с34=2.
Пропускна спроможність розрізу R1 дорівнює 1+ 4 + 2 = 7.
Розріз R2: (1,2), (1,4), (1,3)
с12=3 с14=1 с13= 5.
Пропускна спроможність розрізу R2 дорівнює 3 + 1+ 5 = 9.
Розріз R3: (1,2), (1,4), (2,3), (3,2), (3,4)
с12=3 с14=1 с23= 3 с32= 4 с34= 2.
Пропускна спроможність розрізу R3 дорівнює 3 + 1+ 3 + 4 + 2 = 13.
Розріз R4: (1,3), (3,2), (2,3), (1,4), (2,4)
с13=5 с32= 4 с23= 3 с14=1 с24= 4.
Пропускна спроможність розрізу R4 дорівнює 5 + 4 + 3 +1 + 4 = 17.
Дамо деякі означення.
1 Течією по дузі (i,j) називається невід’ємна цілочислова величина fij ≥ 0, яка менше чи дорівнює пропускній спроможності дуги, тобто fij ≤ cij.
2 Дуга називається ненасиченою, якщо течія через неї менше її пропускної спроможності, тобто fij < cij.
3 Дуга називається насиченою, якщо fij = cij.
Будемо вважати, що в мережі задано течію, якщо:
1) для будь–якої проміжної вершини (не початкової і не завершальної) кількість продукту, що надійшла і що відправляється, рівні;
2) кількість продукту, що відправляється з початкової вершини (джерела) дорівнює кількість продукту, що прибув у завершальну вершину.
Таким чином, течія в проміжних вершинах нічого не лишає і приносить на вихід стільки одиниць товару (інформації), скільки вийшло з входу. Ця кількість і є величина течії.
Величина течії в одній і тій же мережі може бути різною.
Наприклад, розглянемо орієнтований граф

1) f12 = 5 
Таким чином, через даний граф пройшла течія, що дорівнює 5 одиниць продукту: f = 5.
2) f12 = 5 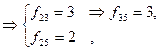
f14 = 2  .
.
Таким чином, через даний граф пройшла течія, що дорівнює f = 3 + 2 + 2 = 7 одиниць продукту.
3) f13 = 3  ,
,
f12 = 5  ,
,
f14 = 2  .
.
Таким чином, через даний граф пройшла течія, що дорівнює
f = 3 + 5 + 2=10 одиниць продукту.
Задача про максимальну течію складається з того, щоб знайти течію найбільшої величини, яку можна пропустити через задану мережу.
Теорема Форда – Фалкерсона.
Для кожної мережі величина максимальної течії дорівнює пропускній спроможності мінімального розрізу.
Введемо в розгляд деякі поняття.
Дуги графа можна віднести до двох категорій:
- дуги, в яких течію можна збільшити, − це ненасичені дуги, їх об’єднаємо в множину І – множина ненасичених дуг;
- дуги, в яких течію можна зменшити, − це невільні дуги, їх об’єднаємо
в множину R – множина обернених дуг.
Дуга, в якій течія дорівнює нулю, називається вільною. В такій дузі течію зменшити не можна.
Дуга може належати і множині І, і множині R одночасно.
Введемо в розгляд величини:
1) і(х,у) =сху - fxy − це максимальна величина, на яку можна збільшити течію в дузі.

На рисунку маємо ланцюг, що збільшує, він містить прямі дуги (1,2), (2,3), (3,4). Течію з вершини 1 в вершину 4 можна збільшити на min(i(1,2), i(2,3), i(3,4)) = min (3;2;1) = 1;
2) r(x,y) − максимальна величина, на яку можна зменшити течію в дузі

На рисунку маємо ланцюг, що збільшує, який містить обернені дуги. Зменшення течії з вершини 4 до вершини 1 приводить до збільшення течії з вершини 1 до вершини 4. У мережі на рисунку течія з вершини 4 у вершину 1 може бути зменшена на min(r (2,1), r (3,2), r (4,3)) = min (1;2;1) = 1, і тим самим течію з вершини 1 у вершину 4 збільшимо на 1.
Сформулюємо алгоритм пошуку ланцюга, що збільшує.
Крок І Визначимо склад множин І і R. Зафарбуємо початкову вершину.
Крок ІІ Будемо зафарбовувати дуги і вершини відповідно до наведених нижче правил доти, поки або не буде зафарбована кінцева вершина, або
фарбування нових вершин стане неможливим.
Правило фарбування.
Якщо вершина х зафарбована, тоді фарбування вершини у і дуги (х,у) відбувається таким чином:
а) якщо дуга (х,у) 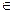 І, то зафарбовується вершина у і дуга (х,у)
І, то зафарбовується вершина у і дуга (х,у)
|

б) якщо дуга (у,х) 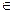 R, тоді зафарбовується вершина у і дуга (у,х)
R, тоді зафарбовується вершина у і дуга (у,х)

в) інших випадках вершина у і дуга (х,у) не фарбуються.
Можна довести, що, якщо кінцева вершина зафарбована, тоді в мережі знаходиться єдиний ланцюг з початкової вершини у кінцеву, який включає зафарбовані дуги (це ланцюг, що збільшує). Якщо кінцева вершина не зафарбована, тоді в мережі відсутні ланцюги з початкової до кінцевої вершини, що збільшують.
Зауваження.
Дуга фарбується лише тоді, коли одна з її вершин зафарбована, а інша ні. Отже не може бути зафарбована дуга, обидві вершини якої були раніше зафарбовані. Тому зафарбовані дуги не можуть утворювати цикл. Зафарбовані дуги утворюють дерево. Якщо зафарбовується кінцева вершина, то існує ланцюг з початкової вершини в кінцеву. Це і буде ланцюг, що збільшує, оскільки процедура фарбування гарантує, що прямі дуги цього ланцюга збільшують, а обернені – зменшують течію в мережі.
Далі розглянемо алгоритм пошуку максимальної течії у графі.
Ідея, що лежить в основі цього алгоритму Форда – Фалкерсона така: беремо деяку початкову течію з початкової в кінцеву вершину і за допомогою алгоритму пошуку ланцюга, що збільшує, виконуємо пошук такого ланцюга. Якщо він виявляється успішним, то течія вздовж знайденого ланцюга збільшується до максимально можливого значення. Потім знаходять новий ланцюг, що збільшує. Якщо на якомусь етапі цієї процедури ланцюг, що збільшує, знайти не вдається, виконання алгоритму закінчується, тобто знайдена течія з початкової до кінцевої вершини є максимальною.
Крок І Беремо будь-яку початкову течію з початкової до кінцевої вершини, наприклад, нульову.
Крок ІІ Сформуємо множини дуг І і R. На цих множинах застосуємо алгоритм пошуку ланцюга, що збільшує.
Якщо ланцюг, що збільшує, знайти не вдається, закінчуємо процедуру алгоритму. У протилежному випадку здійснюємо максимально можливе збільшення течії вздовж цього ланцюга і повертаємось до кроку ІІ.
Приклад.Знайти максимальну течіюу графі при даних пропускних спроможностях дуг в мережі.

1Пропустимо через всі дуги мережі нульову течію.
2Всі дуги мережі відносяться до множини І. Розглянемо ланцюг, що збільшує
(1,2), (2,3), (3,5)
і(1,2) = 2 – 0 = 2 і(2,3) = 3 – 0 = 3 і(3,5) = 2 - 0 =2.
Через цей ланцюг можна пропустити течію, що дорівнює min( 2;3;2) = 2.
Течія в дугах даного ланцюга збільшується на дві одиниці.

Повертаємось до кроку ІІ.
3Знову шукаємо ланцюг, що збільшує. Зауважимо, що дуги (1,2) і (3,5) належать до множини R. Розглянемо ланцюг
(1,3), (2,3), (2,4), (4,5)
І R І І
і(1,3) = 3 – 0 = 3 r(2,3) = 2 і(2,4) = 4 - 0 = 4 і(4,5) = 1 - 0 = 1.
Тепер течія через мережу буде дорівнювати 2 + 1 = 3.

Це максимальна течія, тому що ланцюг, що збільшує, побудувати вже не можна, бо у кінцеву вершину ведуть дуги, що належать до множини R, у яких течію можна лише зменшувати.
Далі розглянемо метод знаходження максимальної течії в неорієнтованому графі.
Маємо неорієнтований граф.


1 По Av1v2B можна пропустити течію, що дорівнює min(5,2,6) = 2. Ребро з мінімальною спроможністю (v1,v2) вилучається, із решти пропускних спроможностей віднімаємо число 2.

2 По Av3v4B можна пропустити течію, що дорівнює min(2,3,2) = 2. Повторюємо процедуру пункту 1.

3 По Av4v2B можна пропустити течію, що дорівнює min(3,4,4) = 3. Тоді одержуємо:
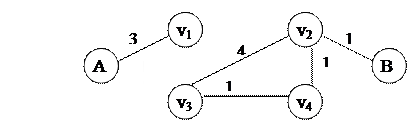
Шляхів із А в В немає. Течія із А в В дорівнює 2 + 2 + 3 = 7.
Питання для самоперевірки
1 Сформулюйте означення графа.
2 Сформулюйте означення орієнтованого та неорієнтованого графа.
3 Сформулюйте означення маршруту у графі.
4 Сформулюйте означення ланцюга, ланцюга простого, цикла, простого цикла, шляха, контура у графі.
5 Який граф називається ейлеровим, гамільтоновим?
6 Що таке матриця суміжності вершин графа?
7 Що таке матриця суміжності ребер (дуг графа)?
8 Що таке матриця інцидентності графа?
9 Дайте означення остовного дерева графа.
10 Як підрахувати число остовних дерев графа?
11 Сформулюйте алгоритм побудови остовного дерева графа, остовного дерева максимальної та мінімальної довжини.
12 Сформулюйте алгоритм Дейкстри побудови найкоротшого шляху в графі.
13 Сформулюйте метод поміток побудови найкоротшого та найдовшого шляху в графі.
14 Дайте означення мережевого графа.
15 Сформулюйте правила, яких необхідно дотримуватись при побудові мережевого графа.
16 Як на мережевому графі відображаються роботи (операції проекта)?
17 Що таке найбільш ранній і найбільш пізній термін настання події?
18 Як їх обчислити?
19 Що таке повний, вільний та незалежний резерв часу операції? Чи є зв’язок між ними?
20 Що таке критична операція?
21 Що таке критичний шлях у мережевому графі?
22 Дайте означення розбивальної множини графа та розрізу графа.
23 Що таке пропускна спроможність розрізу? Що таке мінімальний розріз?
24 Дайте означення течії по дузі.
25 Яка дуга називається насиченою, ненасиченою, вільною?
26 Сформулюйте задачу про максимальну течію в графі.
27 Сформулюйте теорему Форда-Фалкерсона.
28 Сформулюйте алгоритм пошуку ланцюга, що збільшує.
29 Сформулюйте алгоритм пошуку максимальної течії у графі.
Задачі для самостійної роботи
1  Маємо граф
Маємо граф
Побудувати матриці суміжності вершин графа, дуг графа і матрицю інцидентності орграфа.
2Маємо граф
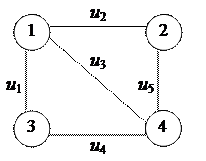 |
Побудувати матриці суміжності вершин і ребер не орграфа.
3За матрицею інцидентності відновити граф.
S= 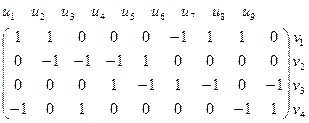
4Маємо граф
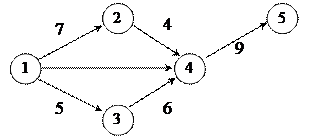
Для цього графа:
а) обчислити кількість остовних дерев графа;
б) побудувати остовне дерево графа, мінімальне остовне дерево і максимальне остовне дерево;
5Маємо граф
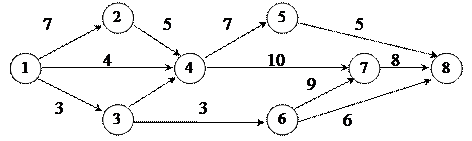 |
Для цього графа обчислити:
а) найкоротший шлях методом Дейкстри;
б) найкоротший та найдовший шлях методом поміток;
в) максимальну течію в графі.
6Маємо проект будівництва спортивної споруди (за нижеподаною таблицею).
| Етап | Робота, що виконується | Попередній етап | Потрібний час (тиж) |
| А | Підготовка будмайданчика | - | |
| Б | Побудова фундаменту | А | |
| В | Підводка магістральних ліній електро- і водопостачання | А | |
| Г | Монтаж вертикальних стін | Б | |
| Д | Монтаж стріха | Г | |
| Е | Укладання дерев’яних перекриттів | Г | |
| Ж | Установка дверей та вікон | Г | |
| З* | Монтаж електрообладнання | Д | |
| І | Монтаж системи опалення | В, Г | |
| К | Установка сантехніки | В, Г | |
| Л | Оздоблювальні роботи | З*, І, К |
За даними проекту побудувати мережевий граф, для кожної роботи (операції) розрахувати повний вільний та незалежний резерви часу, побудувати критичний шлях у графі.
Глава 3 МЕТОД ГІЛОК ТА МЕЖ
Основні поняття
Цей метод буде застосовано для розв’язання задачі про рюкзак та задачі комівояжера.
Сформулюємо основні ідеї метода гілок та меж.
Деяка функція має бути мінімізована f(x)→min, 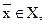 де Х складається з дискретних точок (наприклад, цілочисельних). Це задача нелінійного програмування, навіть якщо f(x) – лінійна функція.
де Х складається з дискретних точок (наприклад, цілочисельних). Це задача нелінійного програмування, навіть якщо f(x) – лінійна функція.
Якщо множина Х складається з невеликої кількості елементів, то можливий перебір всіх елементів, якщо кількість елементів множини Х є великою, то потрібен метод спрямованого перебору. Одним з таких методів є метод гілок та меж . В цьому методі треба вказати дві речі:
1)алгоритм розбиття множини Х;
2)деяку систему оцінок будь-якої підмножини Х.
Множину Х розбиваємо на дві – три частини

Х11, Х12, Х13 – кінцеві множини 1-го кроку.
На другому кроці за деякою ознакою вибираємо одну з множин 1-го кроку і розбиваємо її. Одержані множини разом з нерОзгалуженими множинами другого кроку називаються кінцевими множинами другого кроку.
Для системи оцінок множин запроваджується функція ρ(Х*), 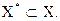 Ця функція повинна задовольняти наступним вимогам:
Ця функція повинна задовольняти наступним вимогам:
1)оцінка будь-якої підмножини ρ(Х*) при розбиті повинна бути меншою, ніж min f(x), 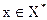 ;
;
2)оцінка будь-якої підмножини повинна бути меншою за оцінку тієї множини, з якої ця підмножина одержана, тобто ρ(Х*) ≥ ρ(Х), 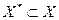 ;
;
з цього випливає, що при розбитті оцінка ρ(Х) не може спадати;
3)оцінка множини, що складається з однієї точки, дорівнює значенню цільової функції f(x) в цій точці.
Ми розглянемо реалізацію метода гілок та меж, яка називається повне галуження.
Для цього на першому кроці обчисляємо оцінку множини Х − ρ(Х) за означеним правилом. Після цього обчислюється оцінка ρ для підмножин Х11, Х12. Зі знайдених оцінок ρ(Х11), ρ(Х12) обирається найменша, і далі галузиться та множина, для якої оцінка ρ найменша. Після цього процедура повторюється.

Далі галузимо ρ(Х12):

З трьох множин Х11, Х21, Х22 вибираємо ту, для якої оцінка є найменшою. Галузимо доти, поки не доберемося до множини, що складається з однієї
точки, оцінок кінцевих множин останнього кроку.
Задача про рюкзак
Є n предметів. Відомі вага p 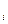 кожного i вартість c
кожного i вартість c 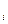 , i =
, i =  .Потрібно покласти у рюкзак сукупність предметів з мінімальноюсумарною вагою за умови, що вартість вантажу не менша за С. Введемо в розгляд змінну
.Потрібно покласти у рюкзак сукупність предметів з мінімальноюсумарною вагою за умови, що вартість вантажу не менша за С. Введемо в розгляд змінну 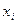 :
:
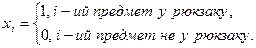
Тоді одержуємо задачу:
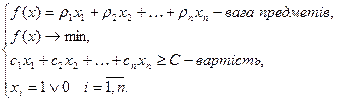
Це повна постановка задачі про рюкзак. Опишемо алгоритм галуження i зв'язану з ним систему оцінок. Для того, щоб обчислити оцінку ρ(х), треба розв’язати задачу лінійного програмування (неперервну), тобто розв’язуємо свою задачу, але умову  замінимо на 0 ≤ хі ≤ 1. Таким чином
замінимо на 0 ≤ хі ≤ 1. Таким чином
ρ(х) =min f(x) за умови 0 ≤ хі ≤ 1. За умови 0 ≤ хі ≤ 1 min f(x) може тільки зменшитися, тобто ρ(x) ≤ minf (x), і вимога на ρ(х) виконана.
Складаємо відношення  – це відносна вага предмета на одиницю вартості. В першу чергу будемо класти в рюкзак ті предмети, що мають min
– це відносна вага предмета на одиницю вартості. В першу чергу будемо класти в рюкзак ті предмети, що мають min  . Умова 0 ≤ хі ≤ 1 означає, що маємо право дробити предмети. При цьому множина припустимих значень збільшується, a min функції може лише зменшуватися.
. Умова 0 ≤ хі ≤ 1 означає, що маємо право дробити предмети. При цьому множина припустимих значень збільшується, a min функції може лише зменшуватися.
Приклад. Маємо п’ять предметів, які треба покласти в рюкзак за умови, що вартість предметів у рюкзаку 
| і |
| |||||||
| сі | вартість | |||||||
| рі | Вага |
Математична модельзадачі така: ми шукаємо min ваги
f(x) = 6х1 + 2х2 + 5x3 + 8х4 +4х5 → min
за умови, що вартість вантажу
10х1 + 5x2 + l 6x3 + 4x4 + 6x5≥ 30. (1)
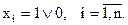
Коли задача буде розв'язана, ми одержимо такий граф-дерево:

Зробимо оцінку планів задачі (1), тобто будуємо оцінку ρ.
 (2)
(2)
Це задача (2) лінійного програмування. Розв'яжемо її.
Розташовуємо предмети в порядку зростання  i відповідно перенумеруємо предмети.
i відповідно перенумеруємо предмети.
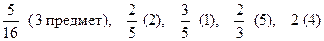
| і | |||||
| поперед. ном. | |||||
| сі | |||||
| рі |
Задача (2) тоді має вигляд (з новою нумерацією предметів):

Якщо візьмемо перший предмет, тоді його вартість 16<30; якщо перший і другий, то їх вартість 16+5=21<30. Якщо візьмемо перший, другий і третій предмети, то їх вартість буде 16 + 5 + 10=31, 31 > 30 на одиницю. Яку частину третього предмета треба взяти? Одиниця – це 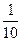 вартості третього предмета, тобто треба взяти
вартості третього предмета, тобто треба взяти 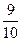 предмета. Тоді опорний план задачі (2): (1; 1; 0,9; 0; 0); ρ(х) = 5 + 2 + б*0,9 = 12,4.
предмета. Тоді опорний план задачі (2): (1; 1; 0,9; 0; 0); ρ(х) = 5 + 2 + б*0,9 = 12,4.
Будемо галузити множину опорних планів по третій координаті, оскільки вона не ціла. Розбиваємо множину Х, тобто сукупність планів задачі (2),на дві підмножини.
З’являються задачі (3) і (4):
 (3)
(3)
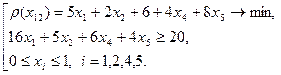 (4)
(4)
Для задачі (3) третього предмета немає.
1пр. + 2пр. + 4пр. 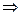 16 + 5 + 6 = 27 < 30,
16 + 5 + 6 = 27 < 30,
1пр. + 2пр. + 4пр.+ 5пр. 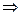 16 + 5 + 6 + 4 = 31 > 30.
16 + 5 + 6 + 4 = 31 > 30.
П’ятий предмет перевищує вартість на одиницю, тобто на 1/4 його вартості, тоді потрібно взяти 3/4 п’ятого предмета. Опорний план для задачі (3) наступний: (1; 1; 0; 1; 3/4),
ρ(х11) = 5 + 2 + 4 + 8*(3/4) = 17.
Розв’язуємо задачу (4):
1 пр. + 2 пр. 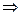 16 + 5 = 21>20.
16 + 5 = 21>20.
Вже другий предмет перевищує вартість на одиницю, тобто на 1/5 його вартості; треба взяти 4/5 другого предмета. Опорний план (1;4/5, 1; 0; 0),
ρ(х12)= 5 + 2*(4/5)+6+0=12,6.
Із ρ(х11) i ρ(х12) вибираємо min, це ρ(х12),і далі галузимо х12 за другою координатою:

З'являються задачі (5) i (6):
 (5)
(5)
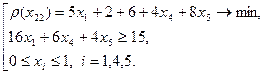 (6)
(6)
Розв’язуємо задачу (5).
1 пр.+ 4 пр. 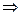 16 + 6 = 22 > 20. Четвертий предмет перевищує вартість на 2 одиниці або на
16 + 6 = 22 > 20. Четвертий предмет перевищує вартість на 2 одиниці або на 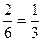 його вартості, тобто потрібно взяти
його вартості, тобто потрібно взяти  четвертого предмету. Опорний план такий: (1; 0; 1;
четвертого предмету. Опорний план такий: (1; 0; 1;  ;0),
;0),
ρ (х21) = 5+6+4*  =13
=13  .
.
Розв’язуємо задачу (6).
1 пр. 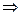 16 > 15. Перший предмет перевищує вартість на 1 одиницю, тобто на
16 > 15. Перший предмет перевищує вартість на 1 одиницю, тобто на  своєї вартості
своєї вартості 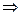 треба взяти
треба взяти 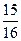 від першого предмету. Опорний план (6) задачі (
від першого предмету. Опорний план (6) задачі ( 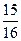 ; 1; 1; 0: 0), ρ(х2,2) =5*
; 1; 1; 0: 0), ρ(х2,2) =5* 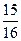 + 2 + 6 = 8 +
+ 2 + 6 = 8 + 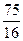 = 12
= 12  .
.
Кінцеві множини цього кроку X11, Х21, Х22
min ρ = ρ(X22) = l2  .
.
Далі треба галузити Х22 за першою координатою: 
Задачі (7) i (8):
 (7)
(7)
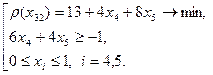 (8)
(8)
Розв’яжемо задачу (7).
4пр.+5 пр. 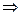 с=10<15
с=10<15 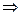 множина планів порожня. Тоді відповідну оцінку вважаємо рівною ∞, тобто ρ(X31) = ∞. Така множина галуженню не підлягає.
множина планів порожня. Тоді відповідну оцінку вважаємо рівною ∞, тобто ρ(X31) = ∞. Така множина галуженню не підлягає.
Розв’язуємо задачу (8). Розв'язок цієї задачі (1;1; 1; 0; 0), ρ(X32) = 13.
Кінцеві множини третього кроку Х11, X21, X31, X32; min ρ = ρ(X3,2) = l3.
План задачі (8) цілочисельний, тому множина Х3,2 розбивається таким чином: одноелементна підмножина Х4,1 = {1,1,1,0,0} – одна точка, i X4,2=X3,2\X4,1. Вважаємо при цьому ρ(Х4,1) = ρ(Х4,2) =ρ(Х3,2) =13. Елемент Х4,1 є розв'язком задачі.
Оптимальне значення цільової функції 13. Якщо перейти до старої
нумерації, тоді в рюкзак треба покласти 3,2 і 1 предмети.
Задача комівояжера
Далі розглянемо іншу задачу, яку можна розв’язати за допомогою методугілок та меж.
Постановка задачі. Маємо n міст, комівояжер повинен відвідати кожне з міст тільки один раз і повернутися в перше. Його маршрут повинен мінімізувати сумарну довжину ( або вартість) пройденого шляху. В теорії графів такий шлях називається гамільтоновим контуром. Тобто задача комівояжера – це знаходження гамільтонового контуру мінімальної довжини.
Мінімізується функція  де Х – множина всіх припустимих маршрутів, тобто гамільтонових контурів, cij – вага дуги (i,j) (довжина або вартість шляху). Будемо вважати крім того, що cii = ∞,
де Х – множина всіх припустимих маршрутів, тобто гамільтонових контурів, cij – вага дуги (i,j) (довжина або вартість шляху). Будемо вважати крім того, що cii = ∞,
cij = ∞, якщо немає шляху з пункту і в пункт j.
Сформулюємо загальну схему розв’язання задачі.
Маємо матрицю С = (cij ), де cij – вага дуги( i,j). Віднімаємо з усіх елементів кожного рядка матриці С мінімальний елемент цього рядка, далі в матриці, що одержана, від усіх елементів кожного стовпця віднімаємо мінімальний елемент цього стовпця. Матриця, що виникає, називається зведеною, позначимо її 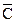 , крім того позначимо через
, крім того позначимо через 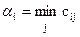 – мінімум в рядку і;
– мінімум в рядку і;  – мінімум у стовпці j;
– мінімум у стовпці j;  – назвемо константами зведення, i,j=1,2,…,n.
– назвемо константами зведення, i,j=1,2,…,n.
Для будь-якого гамільтонового контуру 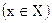 виконується наступне:
виконується наступне: 
У якості ρ(х) вибираємо 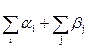 , і тоді виконуються вимоги, які накладаються на оцінку ρ(х), ρ(х) ≤ f(x).
, і тоді виконуються вимоги, які накладаються на оцінку ρ(х), ρ(х) ≤ f(x).
Після операції зведення довжина всіх гамільтонових шляхів зменшуються на одну й ту ж величину, тому оптимальний гамільтонів контур, знайдений з використанням зведеної матриці, буде оптимальним і для початкової матриці.
Множину X ми повинні галузити. Множина Х11складається з уcіx гамільтонових контурів із X, що не містять деякої дуги (r,s). Множила Х12 складається з ycix гамільтонових контурів з X, що містять дугу (r,s).

Правило вибору дуги (r,s) полягає в наступному: оцінку ρ(Х12) прагнуть зробити меншою, оцінку ρ(Х11) – більшою з метою збільшити ймовірність подальшого галуження множини Х12. Бажання зменшити оцінку ρ(Х12) означає, що кандидатами на вибір дуги (r,s) можуть бути лише ті дуги, яким у зведеній матриці 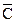 відповідають нульові елементи. Їх може бути декілька. Тоді знайдемо суму констант зведення кожного з нульових елементів матриці
відповідають нульові елементи. Їх може бути декілька. Тоді знайдемо суму констант зведення кожного з нульових елементів матриці 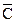 . Позначимо цю суму для елемента (i,j) через Θ(і, j). Як дугу (r,s) вибираємо таку, для якої оцінка знизу максимальна, тобто Θ(r,s) =max Θ (i,j).
. Позначимо цю суму для елемента (i,j) через Θ(і, j). Як дугу (r,s) вибираємо таку, для якої оцінка знизу максимальна, тобто Θ(r,s) =max Θ (i,j).
Наступний етап – побудова зведених матриць i обчислення оцінок знизу.
Замінимо в матриці 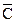 нульовий елемент, що відповіднє дузі (г,s), на ∞. Нову матрицю позначимо С1. Зведена матриця відстаней для гамільтонових контурів із Х11, що не містять дуги (r,s), одержується зведенням матриці C1. Сума констант зведення для матриці С1 дорівнює Θ(r,s).
нульовий елемент, що відповіднє дузі (г,s), на ∞. Нову матрицю позначимо С1. Зведена матриця відстаней для гамільтонових контурів із Х11, що не містять дуги (r,s), одержується зведенням матриці C1. Сума констант зведення для матриці С1 дорівнює Θ(r,s).
Оцінка знизу для функції f(x) на множині Х11 така: ρ(Х11) = ρ(Х) + Θ(r,s).
Гамільтонові контури з Х12 містять дугу (r,s). Викреслимо в матриці 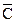 рядок i стовпець, що відповідають дузі (рядок відповідає місту r і стовпець відповідає місту s), Елемент, що відповідає дузі (s,r), замінюємо на ∞ (назад із s в r їхати не можна).
рядок i стовпець, що відповідають дузі (рядок відповідає місту r і стовпець відповідає місту s), Елемент, що відповідає дузі (s,r), замінюємо на ∞ (назад із s в r їхати не можна).
Отриману матрицю позначимо С2 (її розмір менше, ніж у попередньої). Зведена матриця відстаней для контурів з X12 одержується зведенням матриці С2. При цьому оцінка знизу ρ(Х12) = ρ(Х) + τ(r,s), де τ(r,s) – сума констант зведення матриці С2.
Якщо в кожному рядку і стовпцю матриці С1 або С2 виявилося лише по одному елементу, відмінному від ∞, тоді множина X11 (або Х12) містить єдиний маршрут, довжина якого дорівнює ρ(Х11) (або ρ(Х12)).
Приклад. ( Задача комівояжера).
Є 5 міст. Дана матриця відстаней (вартості):
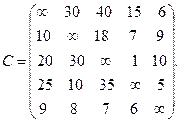
Потрібно знайти гамільтонів контур найменшої довжини.
Розв’язання.
І етап – операція зведення.

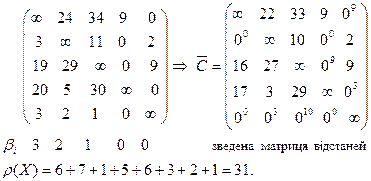 .
.
ІІ етап – операція галуження.
Галуження треба проводити за дугою (5,3):
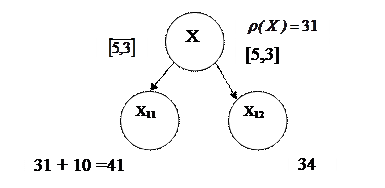

ІІІ етап – побудова зведених матриць.
 .
.
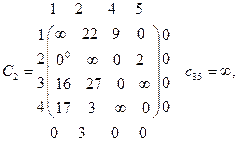
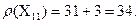
Кінцеві множини першого кроку Х11 і Х12. Галуженню підлягає Х12 ( з мінімальною оцінкою).
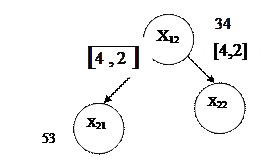
Зведемо матрицю С2:
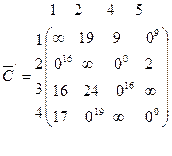 Галуження буде за дугою (4,2).
Галуження буде за дугою (4,2).


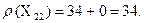
Галуженню підлягає Х22 за дугою (3,4): 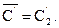
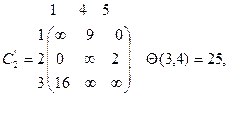
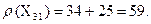
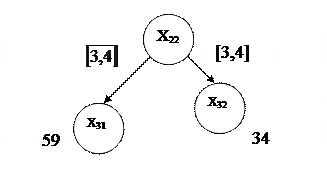


Галуженню підлягає Х32 за дугою (2,1):

Побудуємо отримане дерево:
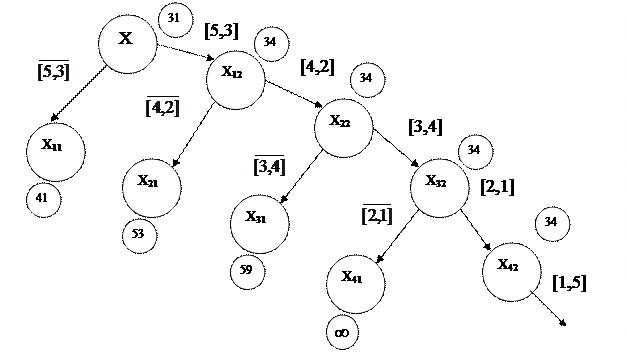
Запишемо гамільтонів контур:


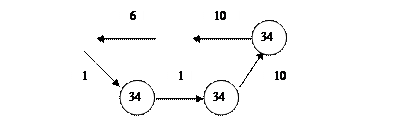
f(x) = 6+7+1+10+10 =34.
Питання для самоперевірки
1 В чому полягає метод гілок та меж?
2 По якому принципу відбувається галуження множини розв’язків?
3 Якій умові повинна відповідати оцінка множин  ?
?
4 Сформулюйте постановку задачі про рюкзак.
5 Яке припущення відносно речей, що кладуть в рюкзак, ми робимо під час розв’язання задачі методом гілок та меж?
6 Сформулюйте постановку задачі комівояжера.
7 У чому полягає алгоритм розв’язання задачі комівояжера?
Задачі для самостійної роботи
1 Розв’язати задачу про рюкзак.
Маємо 5 предметів, де 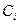 − вартість i-го предмета,
− вартість i-го предмета, 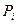 − вага i-го предмета.
− вага i-го предмета.
Дані про предмети наведені в таблиці:
Варіант А
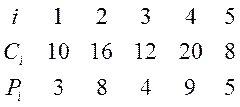 |
С=40
Варіант Б
 |
C=45
2 Розв’язати задачу комівояжера при заданій матриці відстані.
Варіант А Варіант Б
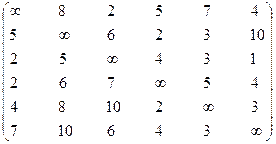 |  |
|
© 2013 wikipage.com.ua - Дякуємо за посилання на wikipage.com.ua | Контакти |